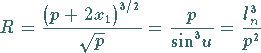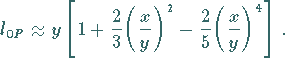Parabel
1. Elemente der Parabel
In der folgenden Abbildung ist die 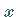 -Achse mit der Parabelachse identisch,
-Achse mit der Parabelachse identisch,
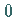 ist der Scheitel der Parabel ,
ist der Scheitel der Parabel , 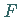 der Brennpunkt der Parabel ,
der sich im Abstand
der Brennpunkt der Parabel ,
der sich im Abstand 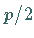 vom Koordinatenursprung auf der
vom Koordinatenursprung auf der 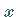 -Achse befindet, wobei
-Achse befindet, wobei 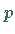 Halbparameter der Parabel genannt wird.
Halbparameter der Parabel genannt wird.
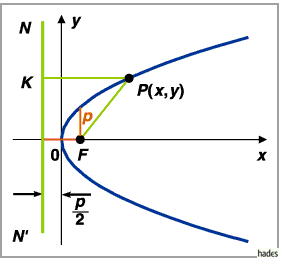
Mit 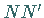 ist die Leitlinie bezeichnet, d.h. eine Gerade, die senkrecht auf der
Parabelachse steht und diese im Abstand
ist die Leitlinie bezeichnet, d.h. eine Gerade, die senkrecht auf der
Parabelachse steht und diese im Abstand 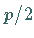 auf der dem Brennpunkt entgegengesetzten
Seite schneidet.
Somit ist der Halbparameter auch gleich der halben Länge der Sehne, die im Brennpunkt
senkrecht auf der Achse steht.
Die numerische Exzentrizität der Parabel ist gleich eins.
auf der dem Brennpunkt entgegengesetzten
Seite schneidet.
Somit ist der Halbparameter auch gleich der halben Länge der Sehne, die im Brennpunkt
senkrecht auf der Achse steht.
Die numerische Exzentrizität der Parabel ist gleich eins.
(S. auch
Leitlinieneigenschaft der Kurven zweiter Ordnung.)
2. Gleichung der Parabel
Wenn der Koordinatenursprung in den Scheitel der Parabel gelegt wird, die 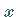 -Achse
mit der Parabelachse zusammenfällt und der Parabelscheitel nach links weisen soll,
dann lautet die Normalform der Parabelgleichung
-Achse
mit der Parabelachse zusammenfällt und der Parabelscheitel nach links weisen soll,
dann lautet die Normalform der Parabelgleichung
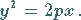 |
(3.364) |
Die Gleichung der Parabel in Polarkoordinaten ist unter
Polargleichung der Kurven 2. Ordnung
zu finden.
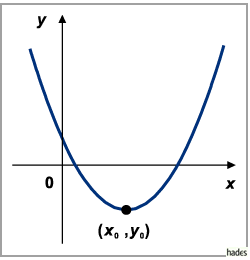
Für Parabeln mit vertikaler Achse lauten die Parabelgleichung und der Halbarameter
dieser so gegebenen Parabel
 |
(3.365a) |
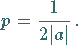 |
(3.365b) |
Ist 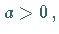 so ist die Parabel nach oben geöffnet, für
so ist die Parabel nach oben geöffnet, für 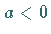 ist sie nach unten
geöffnet.
Die Koordinaten des Scheitels sind
ist sie nach unten
geöffnet.
Die Koordinaten des Scheitels sind
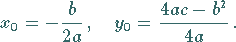 |
(3.365c) |
3. Haupteigenschaft der Parabel (Definition der Parabel)
Die Parabel ist der geometrische Ort aller Punkte 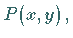 die von einem festen Punkt,
dem Brennpunkt, und einer festen Geraden, der Leitlinie, gleich große Entfernung
besitzen.
die von einem festen Punkt,
dem Brennpunkt, und einer festen Geraden, der Leitlinie, gleich große Entfernung
besitzen.

Hier und in den folgenden Formeln in kartesischen Koordinaten wird die Normalform der
Parabelgleichung angenommen. Dann ist
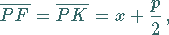 |
(3.366) |
wobei  der vom Brennpunkt ausgehende Radius des Parabelpunktes ist.
der vom Brennpunkt ausgehende Radius des Parabelpunktes ist.
4. Durchmesser der Parabel
Durchmesser der Parabel wird eine Gerade genannt, die parallel zur Parabelachse
liegt.
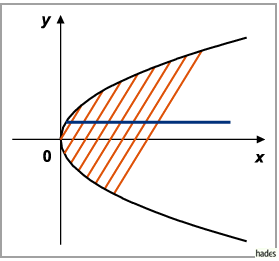
Ein Parabeldurchmesser halbiert die Sehnen, die zur Tangente im Endpunkt des
Durchmessers parallel liegen.
Mit dem Richtungskoeffizienten  der Sehnen lautet die Gleichung des Durchmessers
der Sehnen lautet die Gleichung des Durchmessers
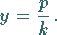 |
(3.367) |
5. Tangente an die Parabel
Die Gleichung der Tangente an die Parabel im Punkt 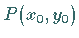 lautet
lautet
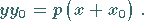 |
(3.368) |
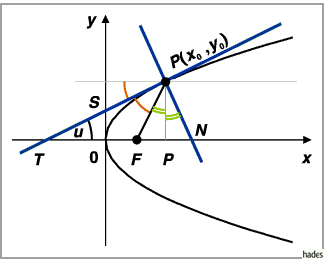
Tangente und Normale der Parabel sind Winkelhalbierende für die Winkel zwischen dem
vom Brennpunkt ausgehenden Radiusvektor und dem Durchmesser des Berührungspunktes.
Die Strecke auf der Parabeltangente zwischen dem Berührungspunkt und dem Schnittpunkt
mit der Parabelachse auf der 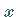 -Achse wird durch die Tangente im Parabelscheitel,
d.h. durch die
-Achse wird durch die Tangente im Parabelscheitel,
d.h. durch die 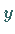 -Achse halbiert:
-Achse halbiert:
 |
(3.369) |
Eine Gerade mit der Gleichung 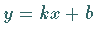 ist eine Tangente an die Parabel, wenn gilt:
ist eine Tangente an die Parabel, wenn gilt:
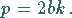 |
(3.370) |
6. Krümmungskreisradius der Parabel
Für den Krümmungskreisradius der Parabel im Punkt 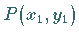 mit
mit
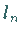 als Normalenlänge
als Normalenlänge 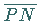 und
und 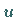 als als Winkel zwischen Tangente
und
als als Winkel zwischen Tangente
und 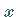 -Achse gilt allgemein
-Achse gilt allgemein
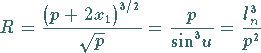 |
(3.371a) |
und speziell im Scheitel 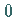 :
:
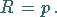 |
(3.371b) |

7. Flächeninhalte in der Parabel
a) Parabelsegment 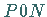 :
:
 |
(3.372a) |
b) Parabelfläche 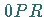 :
:
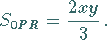 |
(3.372b) |
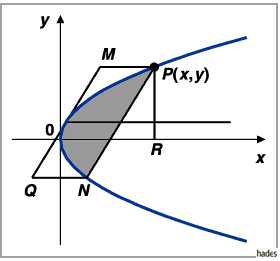
8. Länge des Parabelbogens
Die Länge des Parabelbogens vom Scheitel 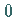 bis zum Punkt
bis zum Punkt 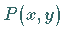 beträgt
beträgt
Für kleine Werte von 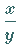 gilt näherungsweise
gilt näherungsweise
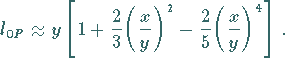 |
(3.373c) |