Kreis
1. Definition
Der Kreis ist der geometrische Ort aller Punkte einer Ebene, die
von einem festen Punkt dieser Ebene, dem Mittelpunkt des Kreises ,
einen konstanten Abstand, den Radius des Kreises, haben
(s. auch Kreis im Unterkapitel Planimetrie).
2. Gleichung des Kreises in kartesischen Koordinaten
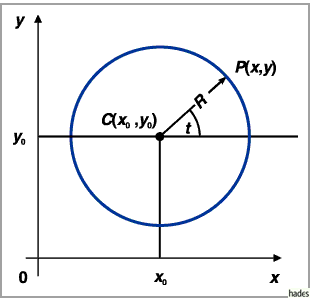
Die Gleichung des Kreises lautet in kartesischen Koordinaten für den in der linken
Abbildung vorliegenden Fall, daß der Kreismittelpunkt im Koordinatenursprung liegt,
 |
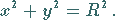(3.335a) |
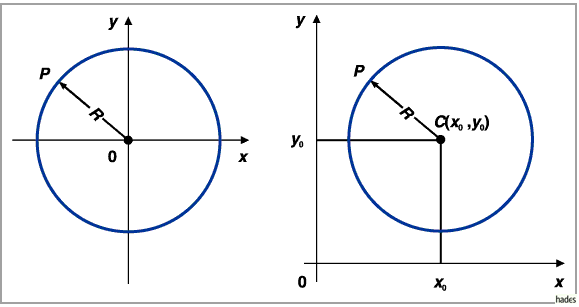
Liegt der Mittelpunkt im Punkt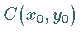 
(rechte Abbildung), dann ergibt sich
 |
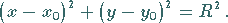(3.335b) |
Die allgemeine Gleichung zweiten Grades
 |
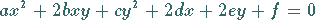(3.336a) |
liefert dann und nur dann einen Kreis, wenn 
und 
.
Für diesen Fall kann die Gleichung stets auf die Form
 |
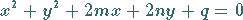(3.336b) |
gebracht werden.
Für den Radius und die Koordinaten des Mittelpunktes gilt dann
 |
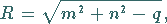(3.337a) |
 |
(3.337b) |
Für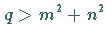 
liefert die Gleichung keine reelle Kurve, für 
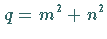ergibt sich ein einziger Punkt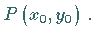 
3. Parameterdarstellung des Kreises
 |
(3.338) |
wobei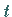 
der Winkel zwischen dem beweglichen Radius und der positiven Richtung der
-Achse ist.
4. Kreisgleichung in Polarkoordinaten
Die Kreisgleichung in Polarkoordinaten lautet ganz allgemein und in
Übereinstimmung mit der linken Abbildung
 |
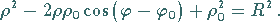(3.339a) |
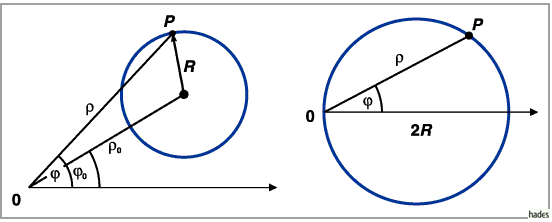
Wenn der Kreismittelpunkt auf der Polarachse liegt und der Kreis durch den
Koordinatenursprung verläuft (rechte Abbildung), dann vereinfacht sich die Gleichung zu
 |
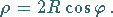(3.339b) |
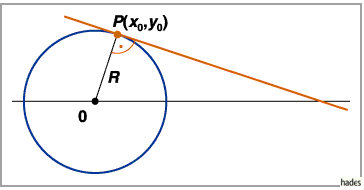
Tangente an den Kreis
Die Tangente an den Kreis mit der Gleichung (3.335a) im Punkt
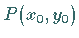(s. die folgende Abbildung) beschreibt die Gleichung
 |
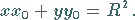(3.340) |
