Themen dieser Seite
Gleichung der Geraden
Jede in den Koordinaten lineare Gleichung definiert eine Gerade, und umgekehrt ist die
Gleichung jeder beliebigen Geraden eine lineare Gleichung ersten Grades.
Allgemeine Geradengleichung:
 |
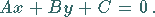(3.321) |
Für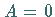 
ist die Gerade eine Parallele zur 
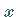-Achse, für 
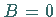eine Parallele
zur 
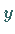-Achse, für 
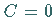verläuft die Gerade durch den Koordinatenursprung.
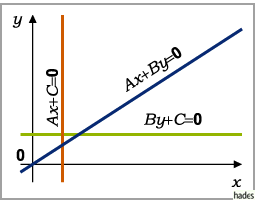
Geradengleichung mit Richtungskoeffizient:
Jede Gerade, die nicht parallel zur 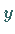-Achse verläuft, kann durch eine Gleichung
der Form
 |
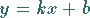(3.322) |
dargestellt werden.
Die Größe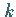 
wird Richtungskoeffizient der Geraden genannt; er ist gleich
dem Tangens des Winkels, den die Gerade mit der positiven Richtung der 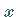-Achse
einschließt.
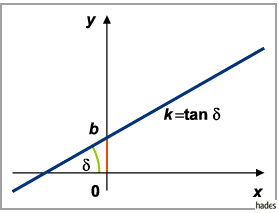
Die Strecke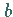 
wird von der Geraden auf der 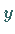-Achse abgeschnitten.
Sie kann ebenso wie der Tangens je nach Lage unterschiedliches Vorzeichen besitzen.
Geradengleichung durch einen vorgegebenen Punkt:
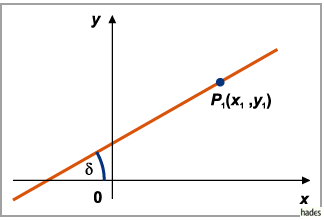
Die Gleichung einer Geraden, welche durch einen vorgegebenen Punkt
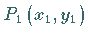in vorgegebener Richtung verläuft, lautet
 |
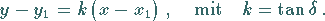(3.323) |
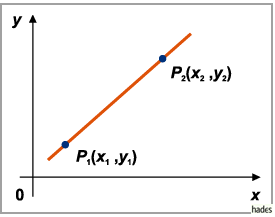
Geradengleichung für zwei vorgegebene Punkte:
Sind zwei Geradenpunkte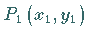 
,
und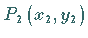 
vorgegeben, dann lautet die Geradengleichung
 |
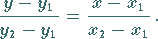(3.324) |
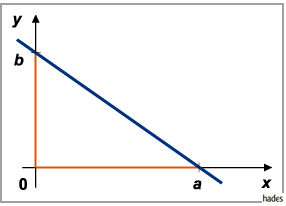
Geradengleichung in Achsenabschnittsform:
Wenn eine Gerade auf den Achsen jeweils die Strecken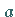 
und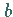
abschneidet, wobei die
Vorzeichen zu berücksichtigen sind, dann lautet ihre Gleichung
 |
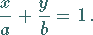(3.325) |
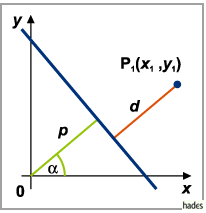
Mit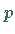 
als Abstand der Geraden vom Koordinatenursprung und 
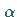als der Winkel, den
die 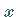-Achse und die vom Koordinatenursprung auf die Gerade gefällte Normale
einschließen, mit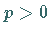 
und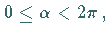 
lautet die
HESSEsche Normalform
 |
(3.326) |
Man kann die HESSEsche Normalform aus der allgemeinen Geradengleichung durch
Multiplikation mit dem Normierungsfaktor
 |
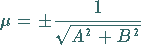(3.327) |
herleiten.
Das Vorzeichen von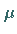 
muß entgegengesetzt zu dem von 
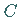gewählt werden.
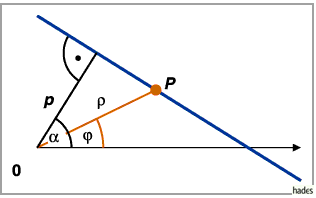
Geradengleichung in Polarkoordinaten:
Mit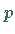
als Abstand vom Pol zur Geraden (Normalenstrecke vom Pol zur Geraden) und
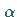als Winkel zwischen Polarachse und der vom Pol auf die Gerade gefällten
Normalen gilt
 |
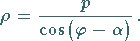(3.328) |
