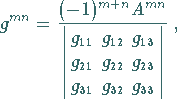Die Darstellung eines skalaren Produkts zweier Vektoren durch seine kontravarianten
Koordinaten liefert Formel (3.294).
Die entsprechende Formel für kovariante Koordinaten lautet
 |
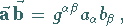(3.304) |
wobei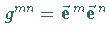 
die metrischen Koeffizienten im
System mit den reziproken Vektoren sind.
Ihr Zusammenhang mit den Koeffizienten 
lautet
 |
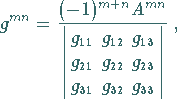(3.305) |
wobei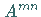 
die Unterdeterminante der im Nenner stehenden Determinante ist; sie
entsteht durch Streichen der Zeile und Spalte des Elements 
Wenn der Vektor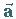 
durch kovariante Koordinaten gegeben ist, der Vektor
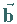dagegen durch kontravariante Koordinaten, dann ist ihr Skalarprodukt gleich
 |
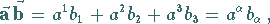(3.306a) |
und analog gilt
 |
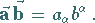(3.306b) |
