|
Das Gradnetz einer Kugel ist auf
einen Zylinder abzubilden, der die Kugel in einem Meridian berührt.
Der Berührungsmeridian und der Äquator bilden die Achsen eines
GAUSS-KRÜGER-Systems.
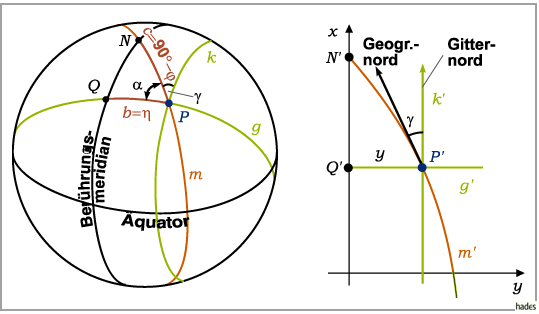
Lösung: Ein Punkt  der Kugeloberfläche wird zu
der Kugeloberfläche wird zu 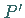 der Ebene.
Der Großkreis g durch
der Ebene.
Der Großkreis g durch  senkrecht zum Berührungsmeridian bildet sich als Gerade
g' senkrecht zur
senkrecht zum Berührungsmeridian bildet sich als Gerade
g' senkrecht zur 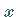 -Achse und der Kleinkreis -Achse und der Kleinkreis 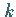 durch
durch  parallel zum
Berührungsmeridian als Gerade
parallel zum
Berührungsmeridian als Gerade 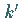 parallel zur
parallel zur 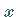 -Achse ab.
Der Meridian -Achse ab.
Der Meridian 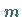 durch
durch  hat als Bild keine Gerade, sondern eine Kurve
hat als Bild keine Gerade, sondern eine Kurve 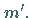 Die nach oben zeigende Richtung der Tangente von
Die nach oben zeigende Richtung der Tangente von 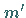 in
in  gibt die
geographische Nordrichtung an, die nach oben zeigende Richtung von
gibt die
geographische Nordrichtung an, die nach oben zeigende Richtung von 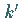 die
geodätische Nordrichtung .
Der Winkel
die
geodätische Nordrichtung .
Der Winkel 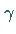 zwischen beiden Nordrichtungen heißt Meridiankonvergenz .
zwischen beiden Nordrichtungen heißt Meridiankonvergenz .
Im rechtwinklig sphärischen Dreieck 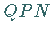 mit
mit 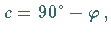 und
und 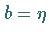 ergibt sich
ergibt sich 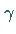 aus
aus 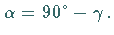 Nach der NEPERschen Regel ist
Nach der NEPERschen Regel ist 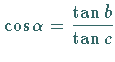 oder
oder
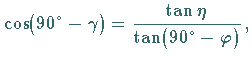
 Da
Da 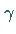 und
und 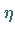 meist klein sind, folgt mit
meist klein sind, folgt mit
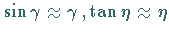 daraus
daraus  Die Längenverzerrung
Die Längenverzerrung 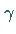 dieses Zylinderentwurfes ist bei kleinen Abständen
dieses Zylinderentwurfes ist bei kleinen Abständen
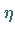 gering, und es kann
gering, und es kann 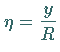 gesetzt werden, wobei
gesetzt werden, wobei
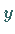 der Rechtswert von
der Rechtswert von  ist.
Man erhält
ist.
Man erhält 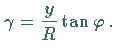 Die Umrechnung von
Die Umrechnung von 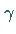 aus dem Bogen- ins Gradmaß ergibt für
aus dem Bogen- ins Gradmaß ergibt für
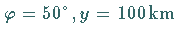 eine Meridiankonvergenz von
eine Meridiankonvergenz von 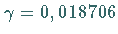 bzw.
bzw. 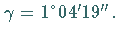
|