Grundaufgaben, Genauigkeitsbetrachtungen
Die verschiedenen Fälle, die bei der Berechnung sphärischer Dreiecke auftreten
können, werden in sogenannte Grundaufgaben eingeordnet.
Für jede Grundaufgabe des schiefwinklig sphärischen Dreiecks sind mehrere
Lösungswege möglich, je nachdem, ob die Lösung nur mit den Grundformeln
(3.190a) bis (3.194b) oder auch mit den Formeln (3.195a) bis
(3.204) erfolgt und ob nur eine Größe im Dreieck oder mehrere Größen
gesucht sind.
Formeln, die die Tangensfunktion enthalten, liefern numerisch genauere Ergebnisse,
besonders im Vergleich zur Berechnung eines Bestimmungsstückes aus der Sinusfunktion,
wenn dessen Wert in der Nähe von 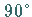 liegt, und aus der Kosinusfunktion, wenn
der Wert des Bestimmungsstückes in der Nähe von
liegt, und aus der Kosinusfunktion, wenn
der Wert des Bestimmungsstückes in der Nähe von 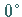 oder
oder 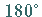 liegt.
Für EULERsche Dreiecke ergeben sich außerdem die aus der Sinusfunktion
berechneten Stücke zweideutig, da die Sinusfunktion in den beiden ersten Quadranten
positiv ist, während die aus den übrigen Funktionen berechneten Stücke eindeutig
erhalten werden.
liegt.
Für EULERsche Dreiecke ergeben sich außerdem die aus der Sinusfunktion
berechneten Stücke zweideutig, da die Sinusfunktion in den beiden ersten Quadranten
positiv ist, während die aus den übrigen Funktionen berechneten Stücke eindeutig
erhalten werden.