Operationen mit Matrizen und Vektoren

Tabelle Operationen mit Matrizen

	die Matrix wird mit dem Skalar multipliziert
	das Produkt der Matrizen und
	die Determinante der Matrix
	die inverse Matrix zu
	die zu transponierte Matrix
	die -te Potenz der Matrix
	die Eigenwerte der Matrix
	die Eigenvektoren der Matrix

Beispiel A
	Es sei Mit die zu transponierte Matrix . Definiert man den allgemeinen vierdimensionalen Vektor mit so erhält man Nun kann das Produkt der Matrix mit dem Vektor gebildet werden, was bekanntlich einen neuen Vektor liefert (s. Rechenoperationen mit Matrizen).

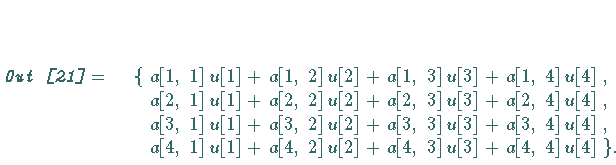
Eine Unterscheidung von Spaltenvektoren und Zeilenvektoren gibt es in Mathematica nicht. Im allgemeinen ist die Matrixmultiplikation nicht kommutativ (s. Rechenoperationen mit Matrizen). Der Ausdruck entspricht in der linearen Algebra dem Produkt einer Matrix mit einem nachfolgenden Spaltenvektor, während dem Produkt eines Zeilenvektors mit einer nachfolgenden Matrix entspricht.

Beispiel B
	Im Abschnitt CRAMERsche Regel ist das lineare Gleichungssystem mit der Matrix und den Vektoren behandelt worden. Da in diesem Fall det ist, kann man das System gemäß sofort lösen. Das geschieht durch