Eine Reihe spezieller (Listen-) Anweisungen steht für die Definition von Vektoren und
Matrizen bereit.
Eine einstufige Liste der Art
 |
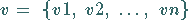(20.13) |
läßt sich jederzeit als Vektor im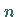 
-dimensionalen Raum mit den Komponenten
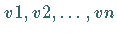auffassen.
Die spezielle Operation 
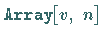erzeugt die Liste (den Vektor)
.
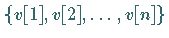Mit Vektoren dieser Art kann symbolische Vektorrechnung betrieben werden.
Die oben eingeführten zweistufigen Listen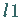 
und
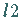können als Matrizen mit den Zeilen 
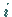und den Spalten 
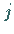aufgefaßt werden.
In diesem Falle wäre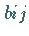 
das Element der Matrix in der 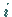-ten Zeile und der 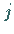-ten
Spalte.
Mit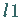
ist eine Rechteckmatrix vom Typ (6,5), mit
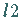eine quadratische Matrix vom Typ
(5,5) gegeben.
Mit der Operation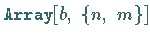 
wird eine Matrix vom Typ 
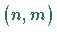erzeugt,
deren Elemente mit 
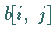gekennzeichnet werden.
Mit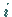
werden die Zeilen numeriert,
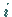läuft von 1 bis 
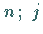numeriert die
Spalten und läuft von 1 bis 
.
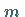In dieser symbolischen Form läßt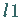
sich darstellen:
 |
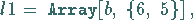(20.14a) |
wobei für die Elemente gilt:
 |
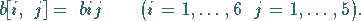(20.14b) |
Die Operation 
erzeugt die 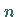-stufige Einheitsmatrix.
Mit der Operation 
wird eine Diagonalmatrix mit den Elementen
von liste auf der Hauptdiagonalen erzeugt.
Die Operation 
gibt die Dimension einer Matrix, deren Struktur
durch liste gegeben ist.
Schließlich erhält man mit 
eine matrixartige Darstellung
von liste .
Eine weitere Möglichkeit zur Definition von Matrizen lautet:
Es sei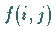 
eine Funktion der ganzen Zahlen
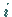und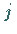 
.
Dann kann mit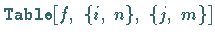 
eine Matrix vom Typ
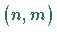definiert werden, deren Elemente die jeweiligen
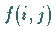sind.
