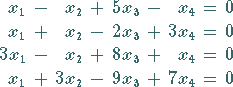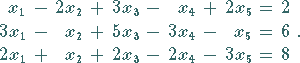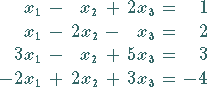Allgemeiner Fall

Beispiel A

Das Beispiel im Abschnitt Triviale Lösung und Fundamentalsystem hat als homogenes System nichttriviale Lösungen, die aus Linearkombinationen von Basisvektoren des Nullraumes der Matrix 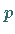bestehen. Das ist jener Teilraum des 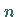-dimensionalen Vektorraumes, der bei Transformationen mit 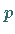auf die Null abgebildet wird. Ein Satz solcher Basisvektoren läßt sich mit der Anweisung erzeugen. Mit der Eingabe erzeugt man die für das System zuständige Matrix, deren Determinante tatsächlich Null ist, was sich mit 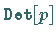überprüfen läßt. Nun wird eingegeben und als Ausgabe erscheint eine Liste mit zwei linear unabhängigen Vektoren des vierdimensionalen Raumes, die im zweidimensionalen Nullraum der Matrix 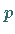eine Basis bilden. Beliebige Linearkombinationen dieser beiden Vektoren liegen ebenfalls im Nullraum, sind also Lösungen des homogenen Gleichungssystems. Ein Vergleich mit der Lösung des betrachteten Beispiels zeigt die Identität.

Beispiel B
	Man erzeugt gemäß Beispiel A aus Abschnitt Allgemeine Regel für das inhomogene System die Matrix , die vom Typ ist und den Vektor Auf die Anweisung erscheint die Meldung Danach wird die Eingabe nochmals ausgegeben.

Beispiel C
	Gemäß Beispiel B aus Abschnitt Allgemeine Regel für das inhomogene System wird eingegeben: Da in diesem Fall das System überbestimmt ist, wird geprüft, ob sich die Matrix aufgrund linearer Abhängigkeiten der Zeilen reduzieren läßt. Mit geschieht das. Danach gibt man ein Die Ausgabe enthält die bekannte Lösung.