Extremwerte von Funktionen
Die Funktion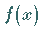 
mit dem Definitionsbereich 
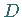hat an der Stelle
ein absolutes oder globales Maximum , wenn
für alle 
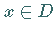gilt:
 |
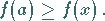(2.8a) |
Die Funktion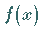
hat an der Stelle
ein relatives oder
lokales Maximum , wenn die Ungleichung (2.8a) nur
in einer Umgebung von
gilt, d.h. für alle 
mit
.
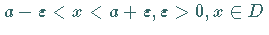Die Definition für ein absolutes oder
globales Minimum sowie für ein relatives oder
lokales Minimum lauten analog,
es ist nur die Ungleichung (2.8a) zu ersetzen durch
 |
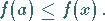(2.8b) |
Hinweise:
1. Die Begriffe Maximum und Minimum, zusammenfassend als Extremwerte
bezeichnet, sind nicht an die Differenzierbarkeit von Funktionen
gebunden, gelten also auch für Funktionen, die an einzelnen Stellen nicht
differenzierbar sind.
Beispiele dafür sind die Spitzen von Kurven.
2. Kriterien zur Bestimmung von Extremwerten bei differenzierbaren Funktionen
findet man unter
Bestimmung von Extremwerten und Wendepunkten.
