Kurve 3. Ordnung, Typ I
Die Funktion
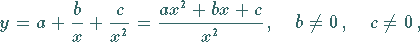 |
(2.47) |
liefert eine Kurve 3. Ordnung . Sie hat die beiden Asymptoten 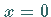 und
und 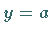 und besteht aus zwei Ästen, von denen der eine einer monotonen Änderung
von
und besteht aus zwei Ästen, von denen der eine einer monotonen Änderung
von 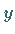 zwischen
zwischen  und
und 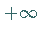 bzw.
bzw. 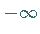 entspricht, während der andere drei
charakteristische Punkte durchläuft:
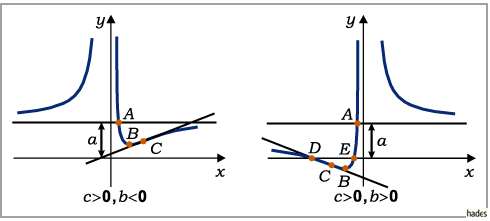
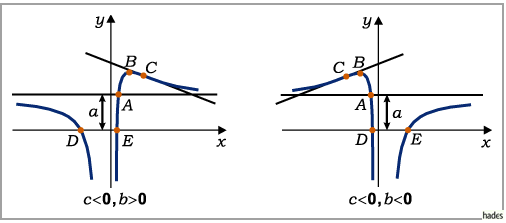
einen Schnittpunkt
entspricht, während der andere drei
charakteristische Punkte durchläuft:
einen Schnittpunkt  mit der Asymptote bei
mit der Asymptote bei 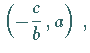 ein Extremum
ein Extremum 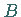 bei
bei 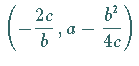 und einen
Wendepunkt
und einen
Wendepunkt 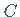 bei
bei 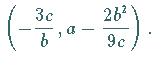 Für die Lage dieser Äste gibt es vier Fälle, die von den Vorzeichen von
Für die Lage dieser Äste gibt es vier Fälle, die von den Vorzeichen von 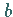 und
und 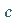 abhängen.
abhängen.
Die Schnittpunkte 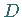 und
und 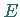 mit der
mit der  -Achse liegen bei
-Achse liegen bei
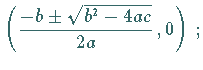 ihre Anzahl kann zwei, eins
(Berührung) oder null betragen, je nachdem, ob für
ihre Anzahl kann zwei, eins
(Berührung) oder null betragen, je nachdem, ob für 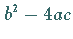 gilt:
gilt: 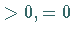 oder
oder 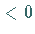 .
Die Funktion (2.47) geht für
.
Die Funktion (2.47) geht für  in die Funktion
in die Funktion 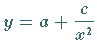 (s. Abbildung der reziproken Potenz)
(s. Abbildung der reziproken Potenz)
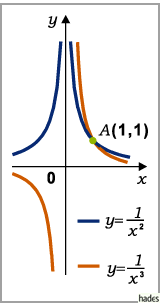
und für  in die gebrochen lineare Funktion
in die gebrochen lineare Funktion 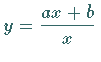 ,
einen
Spezialfall von (2.46), über.
,
einen
Spezialfall von (2.46), über.
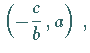 ein Extremum
ein Extremum 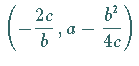 und einen
Wendepunkt
und einen
Wendepunkt 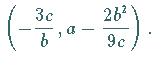 Für die Lage dieser Äste gibt es vier Fälle, die von den Vorzeichen von
Für die Lage dieser Äste gibt es vier Fälle, die von den Vorzeichen von 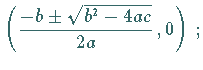 ihre Anzahl kann zwei, eins
(Berührung) oder null betragen, je nachdem, ob für
ihre Anzahl kann zwei, eins
(Berührung) oder null betragen, je nachdem, ob für 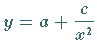 (s. Abbildung der reziproken Potenz)
(s. Abbildung der reziproken Potenz)
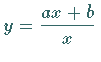 ,
einen
Spezialfall von (2.46), über.
,
einen
Spezialfall von (2.46), über.