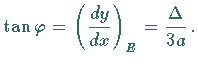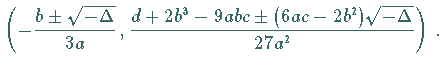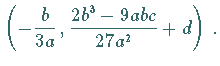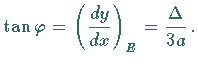Polynom 3. Grades
Die ganzrationale Funktion 3. Grades
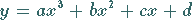 |
(2.42) |
beschreibt in der graphischen Darstellung eine kubische Parabel .
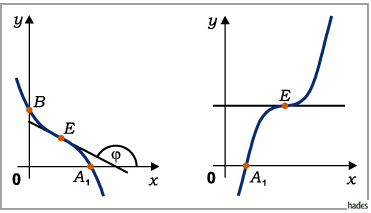
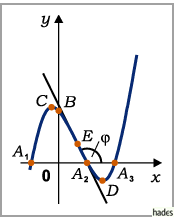
Das Verhalten der Funktion hängt von  und der Diskriminante
und der Diskriminante 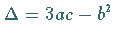 ab.
Wenn
ab.
Wenn 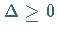 ist (obere linke und rechte Abbildung), dann nimmt die Funktion für
ist (obere linke und rechte Abbildung), dann nimmt die Funktion für
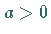 monoton zu, für
monoton zu, für 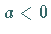 monoton ab.
monoton ab.
Die Funktion besitzt ein Maximum und ein Minimum, wenn 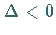 ist (untere Abbildung):
Für
ist (untere Abbildung):
Für 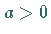 nimmt sie von
nimmt sie von 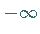 bis zum Maximum zu, dann fällt sie bis zum
Minimum ab, um danach bis
bis zum Maximum zu, dann fällt sie bis zum
Minimum ab, um danach bis 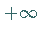 anzusteigen; für
anzusteigen; für 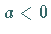 nimmt sie von
nimmt sie von 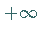 bis zum Minimum ab, steigt danach bis zum Maximum an, um schließlich bis
bis zum Minimum ab, steigt danach bis zum Maximum an, um schließlich bis 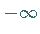 abzufallen.
abzufallen.
Die Schnittpunkte mit der  -Achse lassen sich als reelle Wurzeln von
(2.42) für
-Achse lassen sich als reelle Wurzeln von
(2.42) für 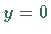 berechnen.
Es kann eine reelle Wurzel geben, zwei (dann gibt es in einem Punkt eine Berührung mit
der
berechnen.
Es kann eine reelle Wurzel geben, zwei (dann gibt es in einem Punkt eine Berührung mit
der  -Achse) oder drei:
-Achse) oder drei: 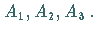 Der Schnittpunkt
Der Schnittpunkt 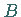 mit der
mit der 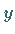 -Achse liegt bei
-Achse liegt bei 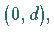 die Extrema
die Extrema 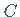 und
und 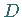 bei
bei
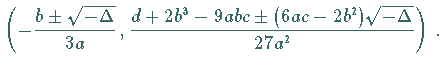
Der Wendepunkt 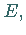 der zugleich Symmetriepunkt der Kurve ist, liegt bei
der zugleich Symmetriepunkt der Kurve ist, liegt bei
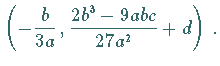
Die Tangente besitzt in diesem Punkt den Richtungskoeffizienten