Grenzwert einer Funktion für x gegen unendlich
Der Definitionsbereich 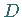 einer Funktion
einer Funktion 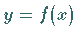 sei
unbeschränkt nach oben bzw. nach unten.
sei
unbeschränkt nach oben bzw. nach unten.
a) Eine Zahl
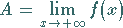 |
(2.20a) |
wird Grenzwert einer Funktion 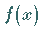 für
für 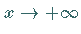 genannt, wenn sich nach Vorgabe
einer positiven Zahl
genannt, wenn sich nach Vorgabe
einer positiven Zahl 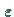 eine Zahl
eine Zahl 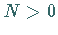 derart angeben
läßt, daß für beliebige
derart angeben
läßt, daß für beliebige 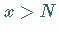 und
und 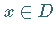 die zugehörigen Werte
von
die zugehörigen Werte
von 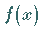 im Intervall
im Intervall 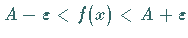 liegen.
In Analogie dazu ist
liegen.
In Analogie dazu ist
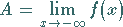 |
(2.20b) |
der Grenzwert einer Funktion 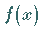 für
für 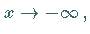 wenn sich nach Vorgabe einer
beliebig kleinen Zahl
wenn sich nach Vorgabe einer
beliebig kleinen Zahl 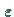 eine Zahl
eine Zahl 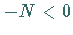 angeben läßt, derart, daß
für beliebige
angeben läßt, derart, daß
für beliebige 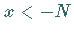 und
und 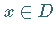 die zugehörigen Werte von
die zugehörigen Werte von 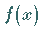 im Intervall
im Intervall
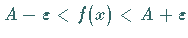 liegen.
liegen.
| Beispiel A |
|
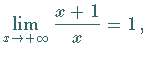
|
| Beispiel B |
|
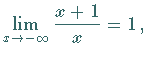
|
| Beispiel C |
|
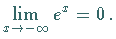
|
b) Wenn allerdings bei unbegrenztem Wachsen oder unbegrenztem Abnehmen
von  die Funktion absolut genommen über alle Grenzen wächst, dann
schreibt man
die Funktion absolut genommen über alle Grenzen wächst, dann
schreibt man
 |
(2.20c) |
| Beispiel A |
|
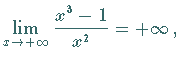
|
| Beispiel B |
|
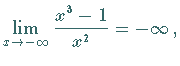
|
| Beispiel C |
|
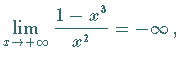
|
| Beispiel D |
|
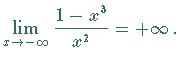
|
![]() die Funktion absolut genommen über alle Grenzen wächst, dann
schreibt man
die Funktion absolut genommen über alle Grenzen wächst, dann
schreibt man