Vollständig durchgerechnetes Beispiel
1. Aufgabenstellung:
Es ist eine empirische Formel für die in der folgenden Tabelle vorgegebene
Abhängigkeit zwischen  und
und 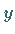 zu suchen.
zu suchen.
Tabelle zur Annäherung empirischer Daten
 |
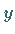 |
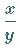 |
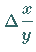 |
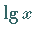 |
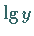 |
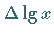 |
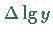 |
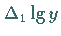 |
 |
| 0,1 |
1,78 |
0,056 |
0,007 |
-1,000 |
0,250 |
0,301 |
0,252 |
0,252 |
1,78 |
| 0,2 |
3,18 |
0,063 |
0,031 |
-0,699 |
0,502 |
0,176 |
+0,002 |
-0,097 |
3,15 |
| 0,3 |
3,19 |
0,094 |
0,063 |
-0,523 |
0,504 |
0,125 |
-0,099 |
-0,447 |
3,16 |
| 0,4 |
2,54 |
0,157 |
0,125 |
-0,398 |
0,405 |
0,097 |
-0,157 |
-0,803 |
2,52 |
| 0,5 |
1,77 |
0,282 |
0,244 |
-0,301 |
0,248 |
0,079 |
-0,191 |
-1,134 |
1,76 |
| 0,6 |
1,14 |
0,526 |
0,488 |
-0,222 |
0,057 |
0,067 |
-0,218 |
-1,455 |
1,14 |
| 0,7 |
0,69 |
1,014 |
0,986 |
-0,155 |
-0,161 |
0,058 |
-0,237 |
- |
0,70 |
| 0,8 |
0,40 |
2,000 |
1,913 |
-0,097 |
-0,398 |
0,051 |
-0,240 |
- |
0,41 |
| 0,9 |
0,23 |
3,913 |
3,78 |
-0,046 |
-0,638 |
0,046 |
-0,248 |
- |
0,23 |
| 1,0 |
0,13 |
7,69 |
8,02 |
0,000 |
-0,886 |
0,041 |
-0,269 |
- |
0,13 |
| 1,1 |
0,07 |
15,71 |
14,29 |
0,041 |
-1,155 |
0,038 |
-0,243 |
- |
0,07 |
| 1,2 |
0,04 |
30,0 |
- |
0,079 |
-1,398 |
- |
- |
- |
0,04 |
2. Auswahl der Näherungsfunktion:
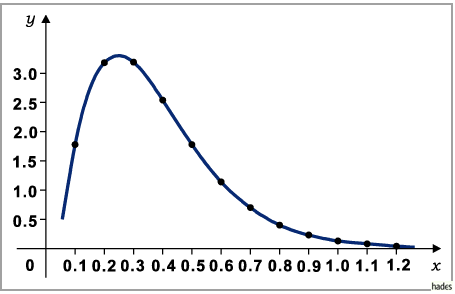
Ein Vergleich der Kurve, die auf der Grundlage der Daten in der Tabelle erhalten wurde
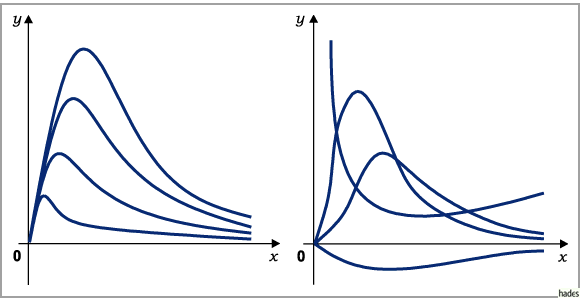
(nächste Abbildung), mit bisher betrachteten Kurven zeigt, daß die Formeln
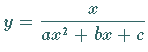 (2.253) oder
(2.253) oder 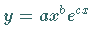 (2.255a) mit
den folgenden Abbildungen geeignet sein könnten.
(2.255a) mit
den folgenden Abbildungen geeignet sein könnten.
3. Parameterbestimmung:
Nimmt man Formel (2.253), dann sind 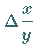 und
und  zu
rektifizieren.
Die Rechnung zeigt aber, daß die Abhängigkeit zwischen
zu
rektifizieren.
Die Rechnung zeigt aber, daß die Abhängigkeit zwischen  und
und
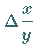 weit entfernt von Linearität ist.
Zur Überprüfung der Eignung von Formel (2.255a) wird die Kurve der
Abhängigkeit
weit entfernt von Linearität ist.
Zur Überprüfung der Eignung von Formel (2.255a) wird die Kurve der
Abhängigkeit 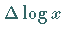 und
und 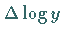 für
für 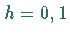 erzeugt sowie die
für
erzeugt sowie die
für 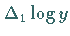 und
und  für
für 
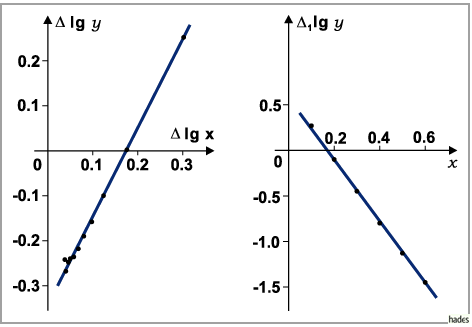
In beiden Fällen ist die Übereinstimmung mit einer Geraden ausreichend, so daß
die Formel 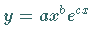 für die Näherung geeignet ist.
Zur Bestimmung der Konstanten
für die Näherung geeignet ist.
Zur Bestimmung der Konstanten 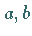 und
und 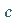 wird eine lineare Abhängigkeit zwischen
wird eine lineare Abhängigkeit zwischen
 und
und 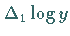 mit der Mittelwertmethode gesucht.
Addition der Bedingungsgleichungen
mit der Mittelwertmethode gesucht.
Addition der Bedingungsgleichungen 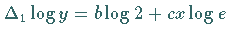 in zwei Gruppen
zu je drei Gleichungen führt auf
in zwei Gruppen
zu je drei Gleichungen führt auf
woraus sich 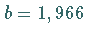 und
und 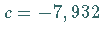 ergibt.
Zur Bestimmung von
ergibt.
Zur Bestimmung von  werden alle Gleichungen vom Typ
werden alle Gleichungen vom Typ
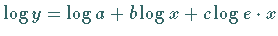 addiert, was
addiert, was 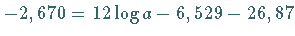 ergibt, so daß aus
ergibt, so daß aus 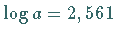 folgt
folgt 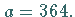 Die mit der Formel
Die mit der Formel 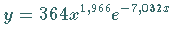 berechneten
berechneten 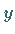 -Werte sind in der
letzten Spalte der obigen Werte-Tabelle als
-Werte sind in der
letzten Spalte der obigen Werte-Tabelle als  angegeben.
Die Fehlerquadratsumme beträgt
angegeben.
Die Fehlerquadratsumme beträgt 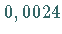 .
Benutzt man die durch Rektifizierung gewonnenen Parameter als Startwerte zur iterativen
Lösung der nichtlinearen Quadratmittelaufgabe
.
Benutzt man die durch Rektifizierung gewonnenen Parameter als Startwerte zur iterativen
Lösung der nichtlinearen Quadratmittelaufgabe
dann erhält man 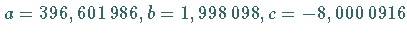 mit der minimalen
Fehlerquadratsumme
mit der minimalen
Fehlerquadratsumme 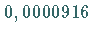 .
.
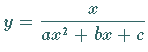 (2.253) oder
(2.253) oder ![]() (2.255a) mit
den folgenden Abbildungen geeignet sein könnten.
(2.255a) mit
den folgenden Abbildungen geeignet sein könnten.