Unendlicher Grenzwert einer Funktion
Das Symbol
 |
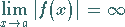(2.17) |
bezeichnet den Fall, daß bei Annäherung von 
an die Stelle 
die
Funktion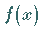 
betragsmäßig über alle Grenzen wächst.
Exakte Formulierung:
Die Gleichung (2.17) gilt, wenn sich nach Vorgabe
einer beliebig großen positiven Zahl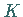 
eine positive Zahl 
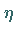derart
angeben läßt, daß für beliebige -Werte im Intervall
 |
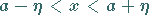(2.18a) |
der entsprechende Wert von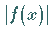 
größer ist als :
 |
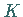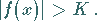(2.18b) |
Wenn dabei alle Werte von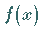
im Intervall
|
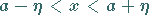(2.18c) |
positiv sind, dann schreibt man
 |
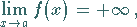(2.18d) |
sind sie negativ, dann gilt
 |
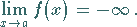(2.18e) |
