Konvergenzkriterium von Cauchy
Damit eine Funktion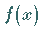 
an der Stelle 
einen Grenzwert besitzt, ist es notwendig
und hinreichend, daß sich die Funktionswerte 
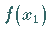und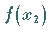 
für zwei
beliebige Werte 
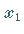und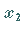 
der unabhängigen Variablen, die zum Definitionsbereich
gehören und in hinreichender Nähe von 
liegen, beliebig wenig voneinander
unterscheiden.
Exakte Formulierung: Damit eine Funktion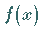
an der Stelle
einen
Grenzwert besitzt, ist es notwendig und hinreichend, daß sich nach Vorgabe einer
beliebig kleinen positiven Zahl 
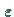eine zweite positive Zahl 
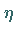angeben
läßt, so daß für zwei beliebige Werte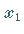
und
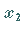aus dem
Definitionsbereich, die den Bedingungen
 |
(2.16a) |
genügen, die Ungleichung
 |
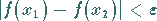(2.16b) |
erfüllt ist.
