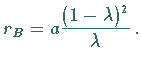Verlängerte und verkürzte Zykloiden oder Trochoiden
Verlängerte und verkürzte Zykloiden oder Trochoiden
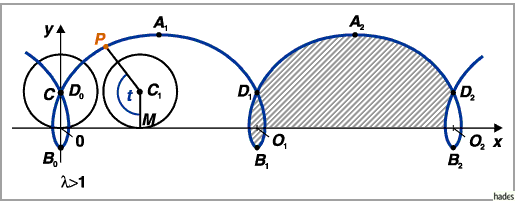
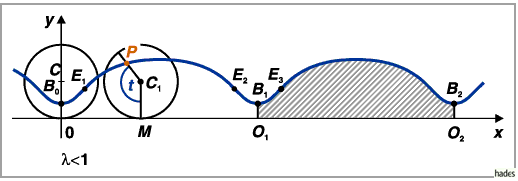
werden von einem Punkt beschrieben, der sich 1. außerhalb oder 2. innerhalb eines
Kreises auf einem vom Kreismittelpunkt ausgehenden und mit dem Kreis fest verbundenen
Strahl befindet, während der Kreis, ohne zu gleiten, auf einer Geraden abrollt.
Die Gleichung der Trochoiden in Parameterform lautet mit  als Radius des Kreises:
als Radius des Kreises:
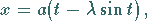 |
(2.232a) |
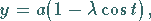 |
(2.232b) |
wobei 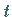 der Winkel
der Winkel 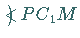 ist.
Wegen
ist.
Wegen 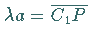 bestimmt
bestimmt 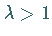 die verlängerte
Zykloide und
die verlängerte
Zykloide und 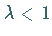 die verkürzte.
die verkürzte.
Die Periode der Kurven ist 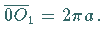
Die Maxima liegen bei 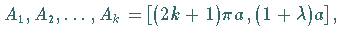 die Minima bei
die Minima bei
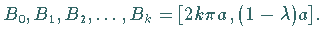
Die verlängerte Zykloide besitzt bei
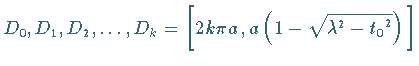 Doppelpunkte, wobei
Doppelpunkte, wobei 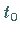 die kleinste
positive Wurzel der Gleichung
die kleinste
positive Wurzel der Gleichung 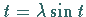 ist.
ist.
Die verkürzte Zykloide besitzt Wendepunkte bei
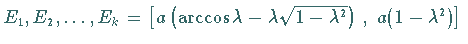 .
.
Die Länge eines Bogens von 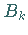 bis
bis 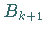 berechnet sich zu
berechnet sich zu 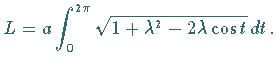
Der Inhalt der in der Abbildung schraffiert gezeichneten Fläche beträgt
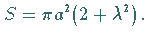
Für den Krümmungsradius erhält man
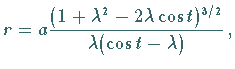 in
den Maxima
in
den Maxima 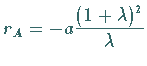 und in den Minima
und in den Minima
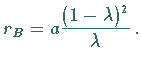
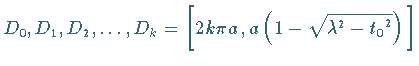 Doppelpunkte, wobei
Doppelpunkte, wobei 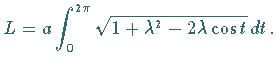
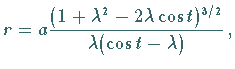 in
den Maxima
in
den Maxima 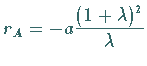 und in den Minima
und in den Minima