Gewöhnliche Zykloide
Gewöhnliche Zykloide wird eine Kurve genannt, die von einem Peripheriepunkt
eines Kreises beschrieben wird, der auf einer Geraden abrollt, ohne zu gleiten.
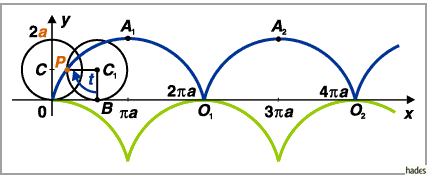
Die Gleichung der gewöhnlichen Zykloide lautet in Parameterform
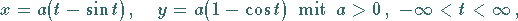 |
(2.231a) |
wobei  der Radius des Kreises und
der Radius des Kreises und 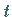 der Wälzwinkel
der Wälzwinkel 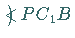 sind, und in
kartesischen Koordinaten
sind, und in
kartesischen Koordinaten
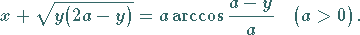 |
(2.231b) |
Die Kurve ist periodisch mit der Periode ( Basis der Zykloide )
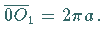
Sie hat Spitzen bei 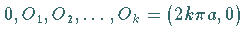 ,
die
Scheitelpunkte
,
die
Scheitelpunkte 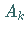 liegen bei
liegen bei
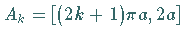 .
.
Die Länge des Bogens 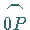 ist
ist 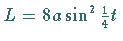 ,
die
Länge eines Zweiges
,
die
Länge eines Zweiges 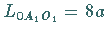 .
.
Der Flächeninhalt beträgt 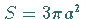 .
.
Der Krümmungsradius ist 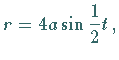 in den Scheiteln
in den Scheiteln
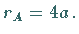
Die Evolute einer Zykloide ist eine
kongruente Zykloide ; sie ist in der Abbildung grün gezeichnet.
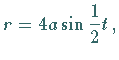 in den Scheiteln
in den Scheiteln