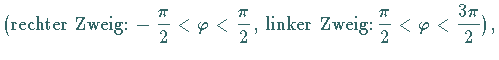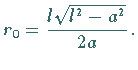Konchoide des NIKOMEDES nennt man den geometrischen Ort aller Punkte  für
die mit
für
die mit 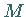 als Schnittpunkt der Verbindungslinie zwischen
als Schnittpunkt der Verbindungslinie zwischen 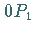 und
und 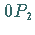 mit der
Asymptote
mit der
Asymptote  die Bedingung
die Bedingung
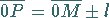 |
(2.221) |
erfüllt ist.
Das Vorzeichen ,, `` gilt für den rechten und ,,
`` gilt für den rechten und ,, `` für den
linken Kurvenzweig.
Die Gleichung der Konchoide des NIKOMEDES in kartesischen Koordinaten, in
Parameterform und in Polarkoordinaten lautet:
`` für den
linken Kurvenzweig.
Die Gleichung der Konchoide des NIKOMEDES in kartesischen Koordinaten, in
Parameterform und in Polarkoordinaten lautet:
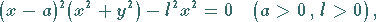 |
(2.222a) |
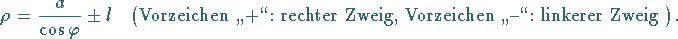 |
(2.222c) |
1. Rechter Zweig:
Die Asymptote ist  ;
der Scheitelpunkt
;
der Scheitelpunkt  liegt bei
liegt bei 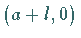 ;
die
Wendepunkte
;
die
Wendepunkte
 haben als
haben als  -Wert die größte Wurzel der Gleichung
-Wert die größte Wurzel der Gleichung
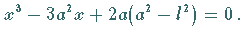
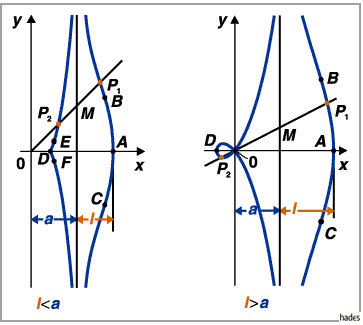
Die Fläche zwischen dem rechten Zweig und der Asymptote ist 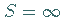 .
.


2. Linker Zweig:
Die Asymptote ist  ;
der Scheitelpunkt
;
der Scheitelpunkt 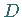 liegt bei
liegt bei 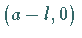 .
Der Ursprung ist ein singulärer Punkt, dessen Charakter von
.
Der Ursprung ist ein singulärer Punkt, dessen Charakter von  und
und 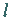 abhängt:
abhängt:
a) Für 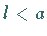 ist es ein isolierter Punkt (obere linke Abbildung).
Die Kurve hat dann zwei weitere Wendepunkte
ist es ein isolierter Punkt (obere linke Abbildung).
Die Kurve hat dann zwei weitere Wendepunkte 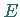 und
und 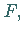 deren Abszisse sich als
zweitgrößte Wurzel der Gleichung
deren Abszisse sich als
zweitgrößte Wurzel der Gleichung 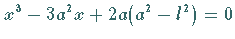 ergibt.
ergibt.
b) Für 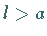 ist der Koordinatenursprung ein Knoten- bzw. Doppelpunkt
(obere rechte Abbildung).
Die Kurve besitzt ein Maximum und ein Minimum an der Stelle
ist der Koordinatenursprung ein Knoten- bzw. Doppelpunkt
(obere rechte Abbildung).
Die Kurve besitzt ein Maximum und ein Minimum an der Stelle
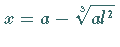 .
.
Die Tangentensteigung beträgt im Koordinatenursprung
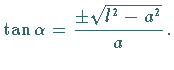
Der Krümmungsradius ist hier 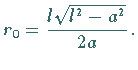
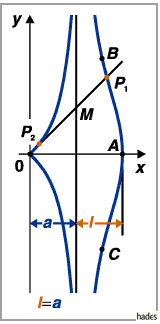
c) Für  wird der Koordinatenursprung zum Rückkehrpunkt
(untere Abbildung).
wird der Koordinatenursprung zum Rückkehrpunkt
(untere Abbildung).