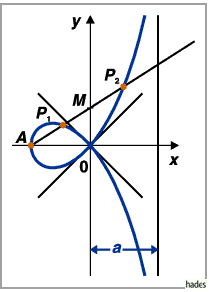
Strophoide
Die Strophoide ist der geometrische Ort aller Punkte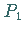 
und 
,
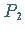die auf einem beliebigen Strahl durch den Punkt 
liegen (
liegt auf der negativen
-Achse) und für die gilt
 |
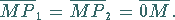(2.219) |
Dabei ist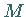 
der Schnittpunkt des Strahles mit der 
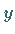-Achse.
Die Gleichung der Strophoide in kartesischen und Polarkoordinaten sowie in Parameterform
lautet:
 |
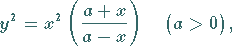(2.220a) |
 |
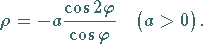(2.220b) |
 |
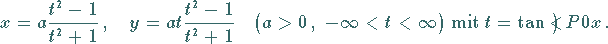(2.220c) |
Der Koordinatenursprung ist ein Doppelpunkt mit den Tangenten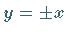 
.
Die Asymptote hat die Gleichung 
,
und der Scheitel
liegt bei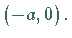 
Der Flächeninhalt der Schleife beträgt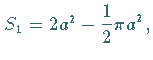 
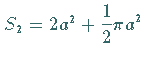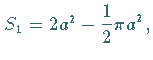der
Flächeninhalt zwischen der Kurve und der Asymptote
.
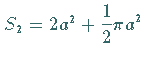