Von der stetigen TSCHEBYSCHEFFschen Approximationsaufgabe
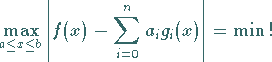 |
(19.202) |
kommt man zur zugehörigen diskreten Aufgabe, indem man 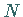 Stützstellen
Stützstellen
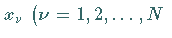 ;
;
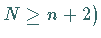 mit der Eigenschaft
mit der Eigenschaft
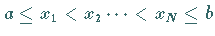 wählt und
wählt und
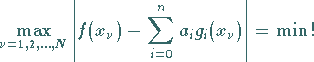 |
(19.203) |
fordert.
Substituiert man
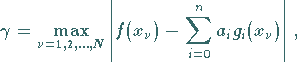 |
(19.204) |
dann folgt daraus unmittelbar
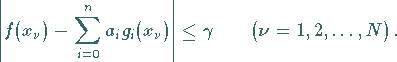 |
(19.205) |
Durch Auflösen der Beträge in (19.205) erhält man ein System von
linearen Ungleichungen für die Koeffizienten 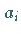 und
und 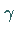 ,
so daß aus
(19.203) die lineare Optimierungsaufgabe
,
so daß aus
(19.203) die lineare Optimierungsaufgabe
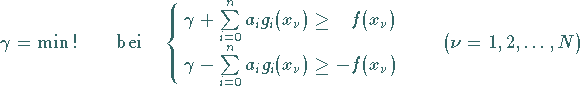 |
(19.206) |
wird. Die Gleichung (19.206) besitzt eine Minimallösung mit 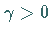 .
Für eine hinreichend große Anzahl
.
Für eine hinreichend große Anzahl 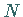 von Stützstellen kann unter bestimmten
Bedingungen die Lösung der diskreten Aufgabe als Näherung für die Lösung der
stetigen Aufgabe angesehen werden.
von Stützstellen kann unter bestimmten
Bedingungen die Lösung der diskreten Aufgabe als Näherung für die Lösung der
stetigen Aufgabe angesehen werden.
Verwendet man an Stelle der linearen Näherungsfunktion
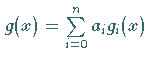 eine Näherungsfunktion
eine Näherungsfunktion
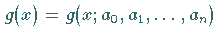 ,
die nichtlinear von den Parametern
,
die nichtlinear von den Parametern
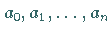 abhängt, dann erhält man in analoger Weise eine
Optimierungsaufgabe, und zwar eine nichtlineare Optimierungsaufgabe, die in der Regel
schon bei einfachen nichtlinearen Ansätzen nicht konvex ist.
Das ist eine wesentliche Einschränkung im Hinblick auf die Wahl numerischer
Lösungsverfahren für
abhängt, dann erhält man in analoger Weise eine
Optimierungsaufgabe, und zwar eine nichtlineare Optimierungsaufgabe, die in der Regel
schon bei einfachen nichtlinearen Ansätzen nicht konvex ist.
Das ist eine wesentliche Einschränkung im Hinblick auf die Wahl numerischer
Lösungsverfahren für
nichtlineare Optimierungsaufgaben.
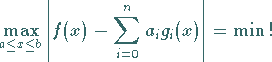
![]() Stützstellen
Stützstellen
![]() ;
;
![]() mit der Eigenschaft
mit der Eigenschaft
![]() wählt und
wählt und
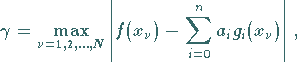
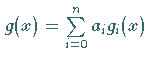 eine Näherungsfunktion
eine Näherungsfunktion