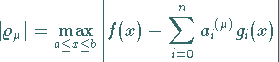Nach REMES geht man zur numerischen Bestimmung der Minimallösung wie folgt vor:
1. Man bestimmt eine Alternantennäherung
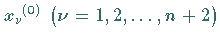 gemäß (19.200), z.B.
gleichabständig oder als Extremstellen von
gemäß (19.200), z.B.
gleichabständig oder als Extremstellen von 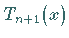 .
.
2. Man löst das lineare Gleichungssystem
und erhält als Lösung die Näherungen 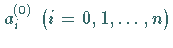 und
und
 .
.
3. Man ermittelt eine neue Alternantennäherung
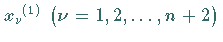 ,
z.B. als Extremstellen der Fehlerfunktion
,
z.B. als Extremstellen der Fehlerfunktion
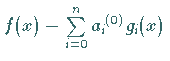 .
Dabei genügt es, Näherungen für diese Extremstellen zu verwenden.
.
Dabei genügt es, Näherungen für diese Extremstellen zu verwenden.
Durch Wiederholung der Schritte 2. und 3. mit 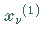 und
und
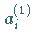 an Stelle von
an Stelle von 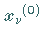 und
und 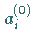 usw. erhält man Folgen von
Näherungen für die Koeffizienten und die Alternantenpunkte, für deren Konvergenz
Bedingungen angegeben werden können (s. Lit. 19.29).
Man kann das Verfahren, das die Grundidee des sogenannten REMES-Algorithmus
wiedergibt, abbrechen, wenn z.B. von einem gewissen Iterationsindex
usw. erhält man Folgen von
Näherungen für die Koeffizienten und die Alternantenpunkte, für deren Konvergenz
Bedingungen angegeben werden können (s. Lit. 19.29).
Man kann das Verfahren, das die Grundidee des sogenannten REMES-Algorithmus
wiedergibt, abbrechen, wenn z.B. von einem gewissen Iterationsindex 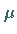 an
an
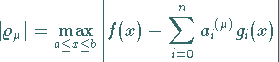 |
(19.201) |
mit hinreichender Genauigkeit gilt.
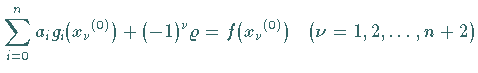
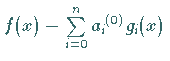 .
Dabei genügt es, Näherungen für diese Extremstellen zu verwenden.
.
Dabei genügt es, Näherungen für diese Extremstellen zu verwenden.