Der Alternantensatz ist der Ausgangspunkt für die numerische Lösung der stetigen
TSCHEBYSCHEFFschen Approximationsaufgabe.
Wählt man als Näherungsfunktion
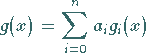 |
(19.198) |
mit 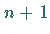 linear unabhängigen, bekannten Ansatzfunktionen, dann sollen mit
linear unabhängigen, bekannten Ansatzfunktionen, dann sollen mit
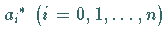 die Koeffizienten der Lösung der
TSCHEBYSCHEFFschen Aufgabe und mit
die Koeffizienten der Lösung der
TSCHEBYSCHEFFschen Aufgabe und mit
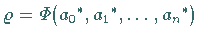 die zugehörige Minimalabweichung
gemäß (19.192) bezeichnet werden.
In dem Fall, daß die Funktionen
die zugehörige Minimalabweichung
gemäß (19.192) bezeichnet werden.
In dem Fall, daß die Funktionen 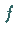 und
und 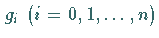 differenzierbar sind, folgt aus dem Alternantensatz
differenzierbar sind, folgt aus dem Alternantensatz
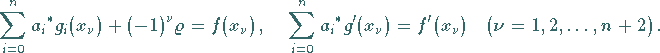 |
(19.199) |
Die Stellen 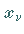 sind Alternantenpunkte mit
sind Alternantenpunkte mit
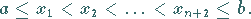 |
(19.200) |
Die Gleichungen (19.199) stellen 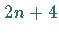 Bedingungen für die
Bedingungen für die 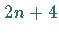 unbekannten
Größen der TSCHEBYSCHEFFschen Approximationsaufgabe dar:
unbekannten
Größen der TSCHEBYSCHEFFschen Approximationsaufgabe dar:
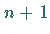 Ansatzkoeffizienten,
Ansatzkoeffizienten, 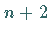 Alternantenpunkte und die Minimalabweichung
Alternantenpunkte und die Minimalabweichung 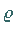 .
Falls die Intervallrandpunkte zu den Alternantenpunkten gehören, brauchen dort die
Bedingungen für die Ableitung nicht zu gelten.
.
Falls die Intervallrandpunkte zu den Alternantenpunkten gehören, brauchen dort die
Bedingungen für die Ableitung nicht zu gelten.
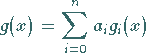
![]() linear unabhängigen, bekannten Ansatzfunktionen, dann sollen mit
linear unabhängigen, bekannten Ansatzfunktionen, dann sollen mit
![]() die Koeffizienten der Lösung der
TSCHEBYSCHEFFschen Aufgabe und mit
die Koeffizienten der Lösung der
TSCHEBYSCHEFFschen Aufgabe und mit
![]() die zugehörige Minimalabweichung
gemäß (19.192) bezeichnet werden.
In dem Fall, daß die Funktionen
die zugehörige Minimalabweichung
gemäß (19.192) bezeichnet werden.
In dem Fall, daß die Funktionen ![]() und
und ![]() differenzierbar sind, folgt aus dem Alternantensatz
differenzierbar sind, folgt aus dem Alternantensatz