Ansatzverfahren
Man macht für die gesuchte Lösung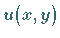 
einen Näherungsansatz der Art
 |
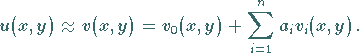(19.139) |
Dabei soll z.B.
1. 
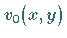die vorgelegte inhomogene Differentialgleichung erfüllen, und alle
übrigen Ansatzfunktionen 
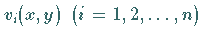sollen die zugehörige
homogene Differentialgleichung erfüllen ( Randmethode ) oder
2.
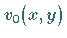den inhomogenen Randbedingungen genügen, und alle übrigen
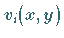
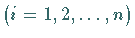sollen den homogenen Randbedingungen genügen
( Gebietsmethode ).
Setzt man die Näherungsfunktion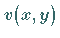 
gemäß (19.139) im ersten Fall
in die Randbedingungen, im zweiten Fall in die Differentialgleichung ein, so wird in beiden
Fällen ein Fehler, der sogenannte Defekt
 |
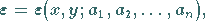(19.140) |
auftreten.
Zur Bestimmung der Ansatzkoeffizient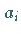en 
kann man nach folgenden Prinzipien verfahren:
