Prinzip des Gaußschen Eliminationsverfahrens
Durch die elementaren Umformungen
1. Vertauschen von Zeilen
2. Multiplikation einer Zeile mit einer von Null verschiedenen Zahl
3. Addition eines Vielfachen einer Zeile zu einer anderen Zeile
wird das System 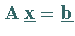 (19.26) in ein
sogenanntes gestaffeltes Gleichungssystem
(19.26) in ein
sogenanntes gestaffeltes Gleichungssystem
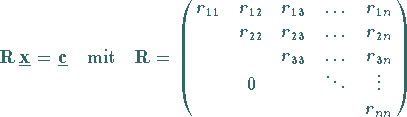 |
(19.27) |
überführt.
Da dabei nur äquivalente Umformungen vorgenommen werden, besitzt
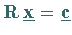 dieselbe Lösung wie
dieselbe Lösung wie 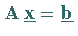 .
Man erhält sie aus (19.27):
.
Man erhält sie aus (19.27):
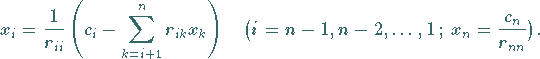 |
(19.28) |
Die durch die Formel (19.28) angegebene Vorschrift nennt man
Rückwärtseinsetzen , da die Gleichungen von (19.27) in der umgekehrten
Reihenfolge ihrer Entstehung benutzt werden.
Der Übergang von 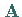 zu
zu  erfolgt in
erfolgt in 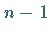 sogenannten
Eliminationsschritten , deren Durchführung am ersten Schritt gezeigt werden soll.
Dieser überführt die Matrix
sogenannten
Eliminationsschritten , deren Durchführung am ersten Schritt gezeigt werden soll.
Dieser überführt die Matrix 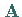 in die Matrix
in die Matrix 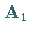 :
:
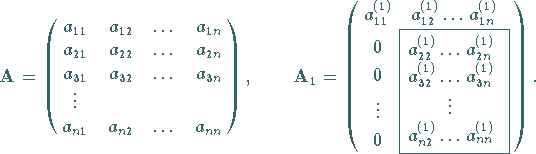 |
(19.29) |
Dabei ist wie folgt vorzugehen:
1. Man bestimme ein 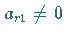 .
Falls kein solches existiert, stop:
.
Falls kein solches existiert, stop: 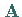 ist singulär.
Andernfalls heißt
ist singulär.
Andernfalls heißt 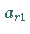 Pivot .
Pivot .
2. Man vertausche die 1. und die 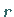 -te Zeile von
-te Zeile von  .
Das Ergebnis ist die Matrix
.
Das Ergebnis ist die Matrix 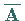 .
.
3. Man subtrahiere für 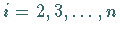 das
das 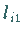 -fache der 1. Zeile von
der
-fache der 1. Zeile von
der 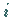 -ten Zeile der Matrix
-ten Zeile der Matrix  .
.
Als Ergebnis erhält man die Matrix 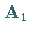 und analog die neue rechte Seite
und analog die neue rechte Seite
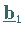 mit folgenden Elementen:
mit folgenden Elementen:
Die in der Matrix 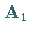 (19.29) eingerahmte Teilmatrix ist vom Typ
(19.29) eingerahmte Teilmatrix ist vom Typ
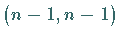 und wird analog zu
und wird analog zu 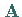 behandelt; usw.
Diese Vorgehensweise bezeichnet man als GAUSSsches Eliminationsverfahren
oder GAUSSschen Algorithmus.
behandelt; usw.
Diese Vorgehensweise bezeichnet man als GAUSSsches Eliminationsverfahren
oder GAUSSschen Algorithmus.
![]() zu
zu ![]() erfolgt in
erfolgt in ![]() sogenannten
Eliminationsschritten , deren Durchführung am ersten Schritt gezeigt werden soll.
Dieser überführt die Matrix
sogenannten
Eliminationsschritten , deren Durchführung am ersten Schritt gezeigt werden soll.
Dieser überführt die Matrix ![]() in die Matrix
in die Matrix ![]() :
:
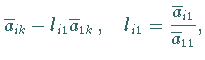
![]() (19.29) eingerahmte Teilmatrix ist vom Typ
(19.29) eingerahmte Teilmatrix ist vom Typ
![]() und wird analog zu
und wird analog zu ![]() behandelt; usw.
Diese Vorgehensweise bezeichnet man als GAUSSsches Eliminationsverfahren
oder GAUSSschen Algorithmus.
behandelt; usw.
Diese Vorgehensweise bezeichnet man als GAUSSsches Eliminationsverfahren
oder GAUSSschen Algorithmus.