Themen dieser Seite
Fehlerarten
Numerische Verfahren sind fehlerbehaftet.
Es gibt die folgenden Fehlerarten, aus denen sich der akkumulierte Fehler (Gesamtfehler)
des Ergebnisses zusammensetzt:
Eingangsfehler
1. Begriff des Eingangsfehlers:
Eingangsfehler heißt der Fehler des Ergebnisses, der durch fehlerbehaftete
Eingangsdaten verursacht wird.
Die Bestimmung des Eingangsfehlers aus den Fehlern der Eingangsdaten wird direkte
Aufgabe der Fehlertheorie genannt.
Als inverse Aufgabe wird jene bezeichnet, die untersucht, welche Fehler die
Eingangsdaten besitzen dürfen, damit ein zugelassener Eingangsfehler des Resultats nicht
überschritten wird.
Die Abschätzung des Eingangsfehlers ist bei komplexeren Aufgaben sehr kompliziert und
kaum durchführbar.
Allgemein gilt für eine zu berechnende reellwertige Funktion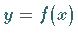 
mit
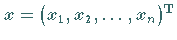für den absoluten Eingangsfehler
wenn man für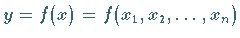 
die
TAYLOR-Formel mit linearem Restglied verwendet.
Mit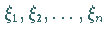 
werden dabei Zwischenstellen, mit
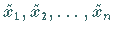Näherungswerte für
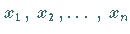bezeichnet.
Unter den Näherungswerten sind hier die fehlerhaften Eingangswerte zu verstehen.
In diesem Zusammenhang ist auch das
GAUSSsche Fehlerfortpflanzungsgesetz zu beachten.
2. Eingangsfehler für einfache arithmetische Operationen:
Für einfache arithmetische Operationen sind die Eingangsfehler bekannt.
Mit den Bezeichnungen
 |
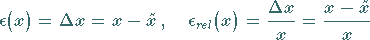(19.276) |
erhält man für die vier Grundrechenoperationen:
 |
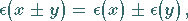(19.277) |
 |
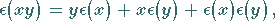(19.278) |
 |
(19.279) |
 |
(19.280) |
 |
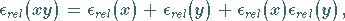(19.281) |
 |
(19.282) |
Die Formeln zeigen: Kleine relative Fehler der Eingangsdaten bewirken bei Multiplikation
und Division nur kleine relative Fehler des Ergebnisses.
Bei Addition und Subtraktion kann dagegen der relative Fehler von Summe und Differenz
groß werden, wenn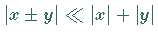 
gilt.
Dann besteht die Gefahr der Stellenauslöschung.
Verfahrensfehler:
1. Verfahrensfehler:
Verfahrensfehler leiten sich aus der Notwendigkeit ab, daß Kontinuum und
Grenzwert numerisch approximiert werden müssen.
Daraus ergeben sich Abbruchfehler bei Grenzprozessen
(wie z.B. bei Iterationsverfahren) und Diskretisierungsfehler bei der Approximation
des Kontinuums durch ein endliches diskretes System (wie z.B. bei der numerischen
Integration).
Verfahrensfehler existieren unabhängig von Eingangs- und Rundungsfehlern; sie können
deshalb nur im Zusammenhang mit dem verwendeten Lösungsverfahren untersucht werden.
2. Verhalten bei bei Iterationsverfahren:
Wird ein Iterationsverfahren zur Lösung eingesetzt, so muß man sich bewußt
sein, daß prinzipiell die beiden Fälle Ausgabe einer richtigen Lösung und Ausgabe
einer falschen Lösung möglich sind.
Es kann jedoch auch der kritische Fall auftreten, daß keine Lösung gefunden wurde,
obwohl eine existiert.
Um Iterationsverfahren transparenter und sicherer zu machen, sollten folgende Empfehlungen
beachtet werden:
a) Um ,,endlose`` Iterationen zu verhindern, sollte die Anzahl der
Iterationsschritte gezählt und in die Abbruchbedingung einbezogen werden (Abbruch nach
einer bestimmten Anzahl von Iterationszyklen auch dann, wenn die geforderte Genauigkeit
noch nicht erreicht wurde).
b) Verfolgung der Lösungsentwicklung auf dem Bildschirm durch die numerische oder
graphische Ausgabe von Zwischenergebnissen.
c) Nutzung evtl. bekannter Eigenschaften der Problemlösung wie Gradient,
Monotonie usw.
d) Untersuchung der Möglichkeit der Skalierung von Variablen bzw. Funktionen.
e) Durchführung mehrerer Tests durch Variation von Schrittweite, Abbruchbedingung,
Startwerten usw.
Rundungsfehler:
Rundungsfehler entstehen dadurch, daß Zwischenergebnisse gerundet werden
müssen.
Sie sind demnach für die Beurteilung eines mathematischen Verfahrens bezüglich der
erzielbaren Genauigkeit der Resultate von wesentlicher Bedeutung.
Sie entscheiden neben den Eingangs- und Verfahrensfehlern darüber, ob ein
numerisches Verfahren stark stabil, schwach stabil oder instabil ist.
Starke Stabilität und schwache Stabilität oder Instabilität liegen vor,
wenn der Gesamtfehler mit wachsender Schrittzahl abnimmt, von gleicher
Größenordnung bleibt oder anwächst.
Bei der Instabilität unterscheidet man die Anfälligkeit gegen Rundungs- und
Diskretisierungsfehler (numerische Instabilität) und gegen Fehler in den
Ausgangsdaten bei exakter Rechnung (natürliche Instabilität).
Ein Rechenprozeß ist dann sinnvoll, wenn die numerische Instabilität nicht
größer als die natürliche Instabilität ist.
Für die lokale Fortpflanzung von Rundungsfehlern, d.h., es werden die Rundungsfehler
betrachtet, die beim Übergang von einem Rechenschritt zum nächsten auftreten, gelten
dieselben Überlegungen und Abschätzungen, wie sie für die Eingangsfehler angestellt
worden sind.
