|
|
|
|
| Beispiel | |
|
Für die Konvertierung der Dezimalzahl | |
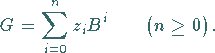 |
(19.255) |
Dividiert man ![]() durch
durch ![]() ,
so erhält man einen ganzzahligen Teil (die Summe) und
einen Rest:
,
so erhält man einen ganzzahligen Teil (die Summe) und
einen Rest:
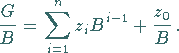 |
(19.256) |
Dabei nimmt ![]() die Werte
die Werte ![]() an und ist die niederwertige Ziffer des
Zahlensystems.
Wendet man das Verfahren jetzt auf die abgespaltete Summe wiederholt an, so ergeben sich
die weiteren Ziffern.
an und ist die niederwertige Ziffer des
Zahlensystems.
Wendet man das Verfahren jetzt auf die abgespaltete Summe wiederholt an, so ergeben sich
die weiteren Ziffern.
b) Gebrochener Teil: Ist ![]() ein echter Dezimalbruch, so lautet die Vorschrift
für die Konvertierung in das Zahlensystem mit der Basis
ein echter Dezimalbruch, so lautet die Vorschrift
für die Konvertierung in das Zahlensystem mit der Basis ![]() jetzt
jetzt
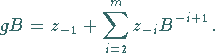 |
(19.257) |
Die wiederholte Anwendung auf die entstehenden Summen liefert die Werte
![]()
| Beispiel A | |
|
Umwandlung der Dezimalzahl 139 in eine Dualzahl: 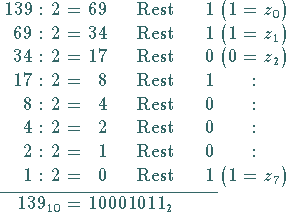
| |
| Beispiel B | |
|
Umwandlung des Dezimalbruchs 0.8125 in einen Dualbruch: 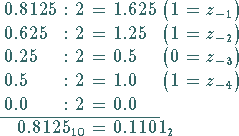
| |
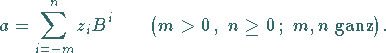 |
(19.258) |
| Beispiel | |
|
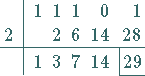
| |
|
|
|