Die Summen, die in den Formeln (19.210) auftreten, kommen auch im Zusammenhang mit
der diskreten FOURIER-Transformation, z.B. in der Elektrotechnik, in der Impuls- und
vor allem in der Bildverarbeitung, vor.
Dabei kann 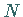 sehr groß sein, so daß die betreffenden Summen äußerst
rationell berechnet werden müssen, denn die Berechnung der
sehr groß sein, so daß die betreffenden Summen äußerst
rationell berechnet werden müssen, denn die Berechnung der 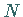 Näherungswerte
(19.210) für die FOURIER-Koeffizienten erfordert etwa
Näherungswerte
(19.210) für die FOURIER-Koeffizienten erfordert etwa 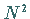 Additionen und
Multiplikationen.
Für den Spezialfall
Additionen und
Multiplikationen.
Für den Spezialfall  läßt sich jedoch mit Hilfe der sogenannten
Schnellen FOURIER-Transformation FFT
(Fast FOURIER-Transformation)
die Anzahl der Multiplikationen von
läßt sich jedoch mit Hilfe der sogenannten
Schnellen FOURIER-Transformation FFT
(Fast FOURIER-Transformation)
die Anzahl der Multiplikationen von 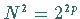 auf
auf 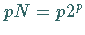 senken.
Die Größenordnung dieser Reduzierung erkennt man an dem folgenden Zahlenbeispiel:
senken.
Die Größenordnung dieser Reduzierung erkennt man an dem folgenden Zahlenbeispiel:
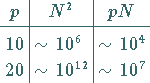 |
(19.215) |
Dadurch sinkt der Rechenaufwand und damit auch die Rechenzeit so stark ab, daß für
einige wichtige Anwendungsgebiete bereits der Einsatz kleinerer Computer ausreicht.
Die FFT nutzt die Eigenschaften der 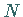 -ten Einheitswurzel, d.h. der Lösungen
der Gleichung
-ten Einheitswurzel, d.h. der Lösungen
der Gleichung 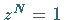 ,
aus, um die Summanden in (19.210)
sukzessiv zusammenzufassen.
,
aus, um die Summanden in (19.210)
sukzessiv zusammenzufassen.
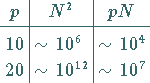
![]() -ten Einheitswurzel, d.h. der Lösungen
der Gleichung
-ten Einheitswurzel, d.h. der Lösungen
der Gleichung ![]() ,
aus, um die Summanden in (19.210)
sukzessiv zusammenzufassen.
,
aus, um die Summanden in (19.210)
sukzessiv zusammenzufassen.