|
|
|
|
verhindert, daß der zulässige Bereich 
bei der Lösung
von (18.102) verlassen wird, indem die Zielfunktion bei Annäherung an den Rand
von
unbeschränkt wächst.
Die Regularitätsbedingung
 |
(18.103) |
sei erfüllt, d.h., das Innere von
ist nicht leer und der Abschluß von 
ist
gleich 
.
Die Funktion 
ist auf
definiert und stetig.
Sie wächst auf dem Rand von
nach 
.
Das Ersatzproblem (18.102) wird mit einer gegen Null fallenden Folge von
Barriereparametern 
gelöst.
Für die Lösung 
des 
-ten Problems (18.102) gilt
 |
(18.104) |
und jeder Häufungspunkt 
der Folge 
ist eine Lösung von
(18.96).
Die folgende Abbildung zeigt eine Veranschaulichung des Barriereverfahrens.
sind z.B. geeignet
| Beispiel | |
|
wird hier nur bezüglich 
gebildet.
Subtraktion beider Gleichungen ergibt  ,
 ,
| |
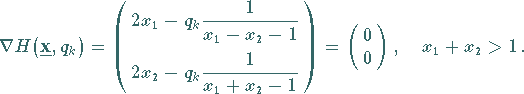
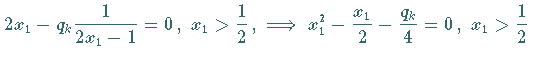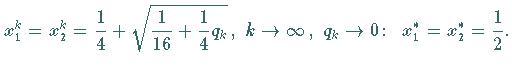
Die Lösung der Aufgaben (18.97) und (18.102)
im -ten Schritt hängt nicht von den Lösungen der vorangegangenen Schritte ab.
Bei der Verwendung großer Straf- bzw. kleiner Barriereparameter treten bei der
Lösung von (18.97) und (18.102) mittels
numerischer Verfahren häufig Konvergenzprobleme auf, falls
keine gute Startnäherung verfügbar ist.
Praktisch nutzt man deshalb den Lösungspunkt des -ten Ersatzproblems als Startwert
der Lösung des (
)-ten Problems.
|
|
,