Verfahren des Goldenen Schnittes und Fibonacci-Verfahren
Das Intervall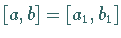 
wird schrittweise so verkleinert, daß das jeweils
neue Teilintervall den Minimalpunkt 
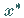enthält.
Im Intervall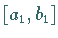 
werden die Punkte
ermittelt.
Das entspricht einer Teilung nach dem Goldenen Schnitt.
Es sind zwei Fälle zu unterscheiden:
Ist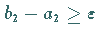 
,
dann wird das Verfahren mit dem Intervall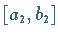 
wiederholt, wobei aber nunmehr einer der Werte 
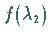(Fall a)) bzw.
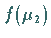(Fall b)) aus dem ersten Schritt verwendet werden kann.
Zur Berechnung eines Intervalls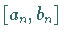 
,
in dem der Minimalpunkt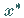
liegt, sind
somit insgesamt 
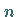Funktionswertberechnungen erforderlich.
Aus der Forderung
 |
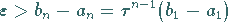(18.69) |
kann eine Abschätzung der notwendigen Schrittzahl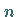
gewonnen werden.
Mit dem Verfahren des Goldenen Schnittes wird höchstens eine Funktionswertberechnung
mehr benötigt als mit dem FIBONACCI-Verfahren .
An Stelle einer Intervallunterteilung gemäß dem Goldenen Schnitt erfolgt hier
eine Unterteilung mit Hilfe der FIBONACCI-Zahlen.
