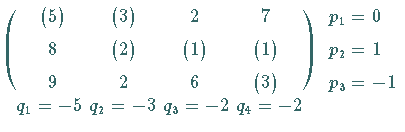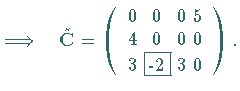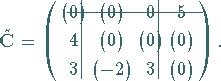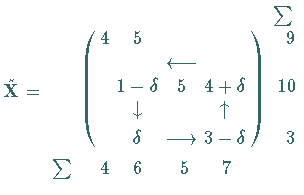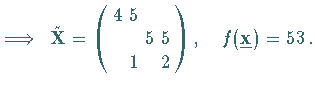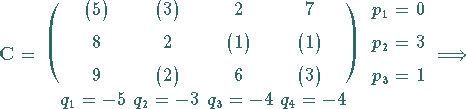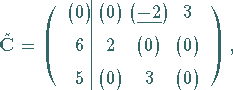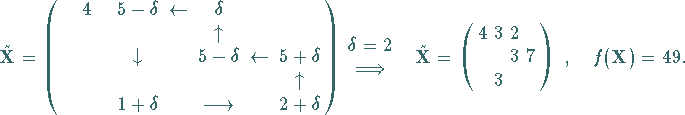Lösung des Transportproblems mit der Potentialmethode
Die Basisvariablen werden iterativ gegen die Nichtbasisvariablen ausgetauscht, um so
jeweils eine zugehörige modifizierte Kostenmatrix zu berechnen.
Der Rechengang wird am Beispiel erläutert.
a) Ermittlung der modifizierten Kostenmatrix 
aus
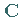mittels
 |
(18.27a) |
unter den Bedingungen
 |
(18.27b) |
Dazu werden in
die zu Basisvariablen gehörenden Kosten markiert und
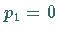gesetzt.
Die weiteren Größen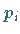 
und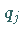 
,
auch Potentiale bzw. Simplexmultiplikatoren
genannt, werden so errechnet, daß zu markierten Kosten gehörende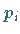
und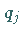 
zusammen mit den Kosten 
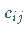die Summe 0 ergeben:
 |
 |
|
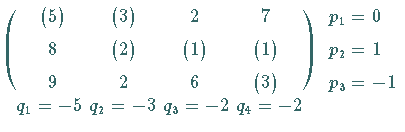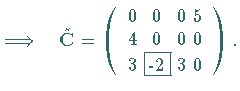(18.27c) |
b) Berechnung von:
 |
(18.27d) |
Ist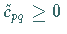 
,
dann ist der gegebene Verteilungsplan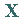 
optimal; anderenfalls wird 
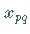als neue Variable gewählt.
Im Beispiel ist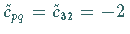 
.
c) In
werden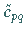 
und die zu Basisvariablen
gehörenden Kosten markiert.
Enthält
eine Zeile oder Spalte mit maximal einem markierten
Element, dann wird diese Spalte oder Zeile gestrichen.
Mit der verbleibenden Restmatrix wird dieser Vorgang wiederholt, bis keine Streichungen
mehr möglich sind.
 |
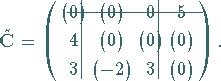(18.27e) |
d) Die zu verbleibenden markierten Elementen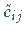 
gehörenden 
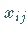bilden einen Zyklus.
Man setzt zunächst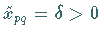 
.
Alle weiteren zu markierten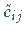
gehörenden 
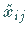werden so
bestimmt, daß die Nebenbedingungen erfüllt bleiben.
Die Größe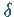 
errechnet sich aus
 |
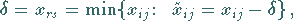(18.27f) |
wobei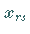 
Nichtbasisvariable wird.
Im Beispiel ist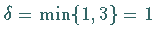 
.
 |
 |
|
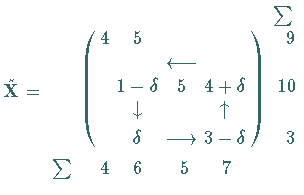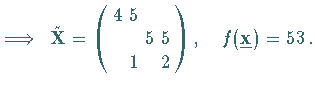(18.27g) |
Danach wird das Verfahren ab Schritt 1 und 
wiederholt.
 |
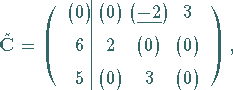(18.27h) |
 |
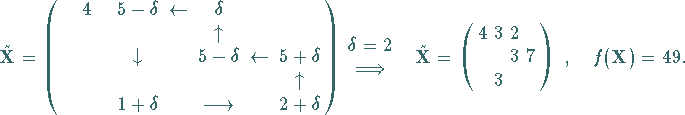(18.27i) |
Die nächste zu bestimmende Matrix
enthält keine negativen
Elemente.
Deshalb ist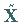 
ein optimaler Verteilungsplan.
