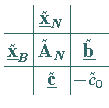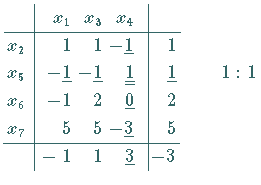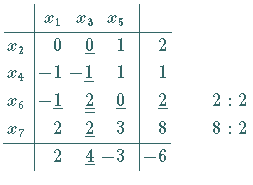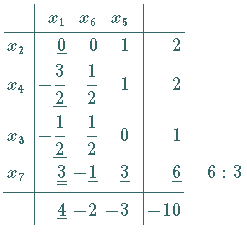|
Die zum Beispiel unter Ecke und Basis gefundene Normalform kann
direkt in ein Simplextableau übertragen werden.
Schema 4a, b
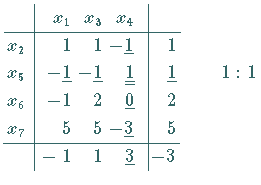
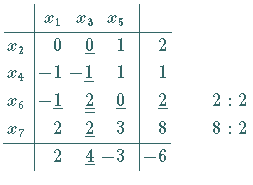 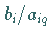 .
Die Quotienten wurden hinter der letzten Spalte des Tableaus notiert.
Der kleinste Quotient legt die Pivotzeile fest.
Ist die Pivotzeile nicht eindeutig zu bestimmen, dann ist die durch das neue Tableau
bestimmte Ecke entartet.
Mit den Austauschregeln erhält man das rechte Tableau.
Dieses Tableau bestimmt die Ecke .
Die Quotienten wurden hinter der letzten Spalte des Tableaus notiert.
Der kleinste Quotient legt die Pivotzeile fest.
Ist die Pivotzeile nicht eindeutig zu bestimmen, dann ist die durch das neue Tableau
bestimmte Ecke entartet.
Mit den Austauschregeln erhält man das rechte Tableau.
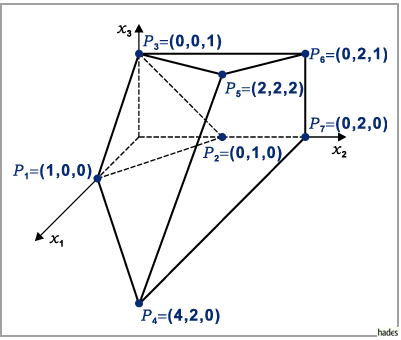
Dieses Tableau bestimmt die Ecke 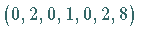 ,
die dem Punkt ,
die dem Punkt 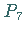 in der Abbildung
entspricht.
in der Abbildung
entspricht.
Da das neue Tableau nicht optimal ist, wird jetzt 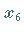 gegen
gegen 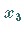 getauscht (nächstes
linkes Schema).
Die Ecke des 3. Tableaus entspricht dem Punkt
getauscht (nächstes
linkes Schema).
Die Ecke des 3. Tableaus entspricht dem Punkt 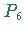 in der Abbildung.
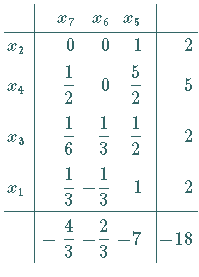
Nach einem weiteren Tausch erhält man ein optimales Tableau (nächstes rechtes Schema)
mit dem Maximalpunkt
in der Abbildung.
Nach einem weiteren Tausch erhält man ein optimales Tableau (nächstes rechtes Schema)
mit dem Maximalpunkt 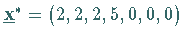 ,
der dem Punkt ,
der dem Punkt 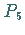 mit dem
maximalen Zielfunktionswert
mit dem
maximalen Zielfunktionswert 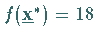 entspricht.
entspricht.
Schema 4c, d
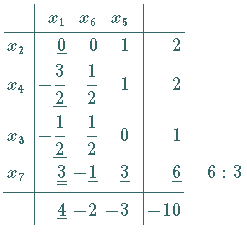
 |