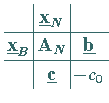Simplextableau
Mit dem Simplexverfahren wird eine Folge von Eckpunkten des zulässigen Bereiches
mit wachsenden Zielfunktionswerten ermittelt.
Der Übergang zu einer neuen Ecke wird vollzogen, indem eine zur gegebenen Ecke
gehörende Normalform zu einer Normalform der neuen Ecke umgewandelt wird.
Zur übersichtlichen Darstellung dieses Vorganges sowie zur Formalisierung der
rechentechnischen Umsetzung wird eine als bekannt vorausgesetzte Normalform
(18.8a,b) in das folgende Simplextableau eingetragen:
Schema 2
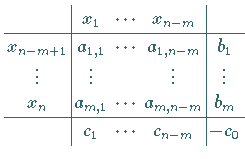
oder kürzer
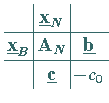
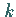 -te Zeile des Tableaus ist zu lesen als
-te Zeile des Tableaus ist zu lesen als
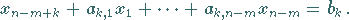 |
(18.14a) |
Für die Zielfunktion gilt
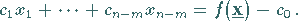 |
(18.14b) |
Aus dem Simplextableau wird die Ecke 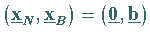 abgelesen.
Gleichzeitig ist der Zielfunktionswert dieser Ecke durch
abgelesen.
Gleichzeitig ist der Zielfunktionswert dieser Ecke durch 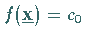 bestimmt.
bestimmt.
Auf jedes Tableau trifft genau einer der drei Fälle zu:
a) 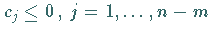 :
Das Tableau ist optimal.
Der Punkt
:
Das Tableau ist optimal.
Der Punkt 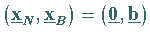 ist der Maximalpunkt.
ist der Maximalpunkt.
b) Für mindestens ein 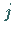 gilt
gilt 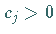 und
und
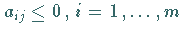 :
Das lineare Optimierungsproblem besitzt keine Lösung, da die Zielfunktion in Richtung
wachsender
:
Das lineare Optimierungsproblem besitzt keine Lösung, da die Zielfunktion in Richtung
wachsender 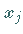 -Werte unbeschränkt wächst.
-Werte unbeschränkt wächst.
c) Für alle 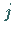 mit
mit 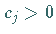 gibt es mindestens ein
gibt es mindestens ein 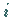 mit
mit 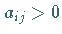 :
Man kann von einer Ecke
:
Man kann von einer Ecke 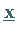 zu einer Ecke
zu einer Ecke 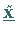 übergehen mit
übergehen mit
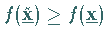 .Für eine nichtentartete Ecke
.Für eine nichtentartete Ecke 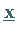 gilt immer das ,,
gilt immer das ,,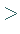 ``-Zeichen.
``-Zeichen.
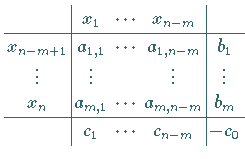 oder kürzer
oder kürzer