|
|
|
|
heißt
minimumvertauschbar , falls gilt:
 |
(18.120) |
Diese Eigenschaft ist zum Beispiel dann erfüllt, wenn 
für jedes
bezüglich des zweiten Argumentes monoton wachsend ist, d.h., wenn
für alle
gilt:
 |
(18.121) |
Für die Kostenfunktion des dynamischen Optimierungsproblems wird nun die Separierbarkeit
von 
und die Minimumvertauschbarkeit aller Funktionen 
,
gefordert.
Folgende häufig Verwendung findende Klassen von Kostenfunktionen genügen beiden Bedingungen:
 |
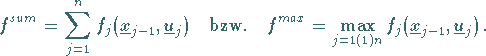(18.122) |
Die Funktionen 
lauten
 |
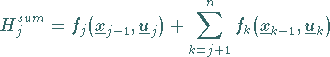(18.123) |
bzw.
 |
(18.124) |
|
|