|
|
|
|
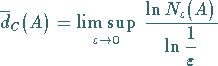 |
(17.41a) |
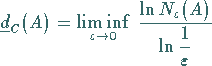 |
(17.41b) |
Für eine beschränkte Menge ![]() kann in den obigen Definitionen die
Zahl
kann in den obigen Definitionen die
Zahl ![]() auch folgendermaßen definiert werden:
Der
auch folgendermaßen definiert werden:
Der ![]() wird mit einem Gitter aus
wird mit einem Gitter aus ![]() -dimensionalen Würfeln der Seitenlänge
-dimensionalen Würfeln der Seitenlänge
![]() überdeckt.
Dann kann für
überdeckt.
Dann kann für ![]() die Anzahl der Würfel des Gitters, die
die Anzahl der Würfel des Gitters, die ![]() schneiden,
genommen werden.
schneiden,
genommen werden.
Wichtige Eigenschaften der Kapazitätsdimension:
(KD1) Es gilt immer ![]() .
.
(KD2) Für ![]() -dimensionale Flächen
-dimensionale Flächen ![]() ist
ist ![]() .
.
(KD3) Mit der Abschließung ![]() von
von ![]() gilt
gilt
![]() ,
während oft
,
während oft ![]() ist.
ist.
(KD4) Ist ![]() so gilt für die Kapazitätsdimension im
allgemeinen nicht
so gilt für die Kapazitätsdimension im
allgemeinen nicht ![]() .
.
| Beispiel | |
|
Sei | |
|
|
|