|
|
|
|
die Differentialgleichung
eine konstante Matrix vom Typ 
ist.
Die Operator-Norm einer Matrix
ist durch
gegeben, wobei für
die Vektoren des
wieder die EUKLIDische Norm
vereinbart sei.
Seien
und 
zwei beliebige Matrizen vom Typ 
.
Dann gilt:
a) 
.
b) 
.
c) 
.
d) 
.
e) 
,
wobei 
der größte
Eigenwert von 
ist.
Die Fundamentalmatrix mit Anfang 
zur Zeit 
von (17.14) ist die
Matrix-Exponentialfunktion
 |
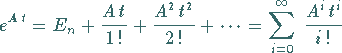(17.15) |
mit folgenden Eigenschaften:
a) Die Reihe für 
konvergiert bezüglich 
auf einem beliebigen
kompakten Zeitintervall gleichmäßig und für jedes
absolut.
b) 
.
c)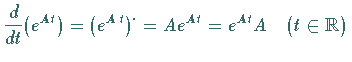 
.
d) 
.
e) 
ist für alle
regulär und 
.
f) Sind
und
kommutative Matrizen vom Typ ,
d.h. gilt 
,
so ist 
und 
.
g) Sind
und
Matrizen vom Typ
und ist
regulär, so ist
.
|
|
