Vertrauensgrenzen für den Mittelwert bei bekannter Streuung
Es sei 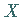 eine kontinuierliche Zufallsgröße, normalverteilt mit den Parametern
eine kontinuierliche Zufallsgröße, normalverteilt mit den Parametern
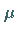 und
und 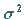 .
Gemäß Abschnitt Verteilung der Stichprobenmittelwerte ist
dann
.
Gemäß Abschnitt Verteilung der Stichprobenmittelwerte ist
dann 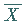 ebenfalls eine kontinuierliche Zufallsgröße, normalverteilt
mit den Parametern
ebenfalls eine kontinuierliche Zufallsgröße, normalverteilt
mit den Parametern 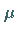 und
und 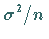 .
Durch die Substitution
.
Durch die Substitution
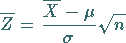 |
(16.136) |
erhält man eine Zufallsgröße 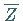 ,
die der normierten Normalverteilung
genügt.
Für diese gilt
,
die der normierten Normalverteilung
genügt.
Für diese gilt
 |
(16.137) |
Gibt man jetzt eine Irrtumswahrscheinlichkeit 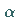 vor und verlangt
vor und verlangt
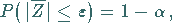 |
(16.138) |
dann kann man 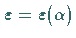 aus (16.137)
numerisch bestimmen bzw. aus der Tabelle Normierte Normalverteilung
ablesen und erhält aus
aus (16.137)
numerisch bestimmen bzw. aus der Tabelle Normierte Normalverteilung
ablesen und erhält aus 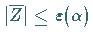 unter Beachtung von
(16.136) die Beziehung
unter Beachtung von
(16.136) die Beziehung
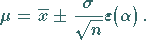 |
(16.139) |
Die Werte 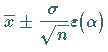 in
(16.139) heißen
Vertrauensgrenzen für den Mittelwert
in
(16.139) heißen
Vertrauensgrenzen für den Mittelwert 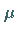 der Grundgesamtheit bei bekannter
Streuung
der Grundgesamtheit bei bekannter
Streuung 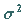 und vorgegebener Irrtumswahrscheinlichkeit
und vorgegebener Irrtumswahrscheinlichkeit 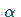 .
Man kann auch sagen:
Der Mittelwert
.
Man kann auch sagen:
Der Mittelwert 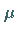 liegt mit der statistischen Sicherheit
liegt mit der statistischen Sicherheit 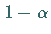 zwischen den
Vertrauensgrenzen (16.139).
zwischen den
Vertrauensgrenzen (16.139).
Hinweis: Ist der Stichprobenumfang hinreichend groß 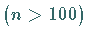 ,
dann kann
in (16.139) an Stelle der in der Regel unbekannten Streuung
,
dann kann
in (16.139) an Stelle der in der Regel unbekannten Streuung 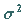 der Grundgesamtheit die Stichprobenstreuung
der Grundgesamtheit die Stichprobenstreuung 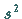 verwendet werden.
Anderenfalls müssen die Vertrauensgrenzen mit Hilfe der
verwendet werden.
Anderenfalls müssen die Vertrauensgrenzen mit Hilfe der 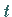 -Verteilung gemäß
(16.142) ermittelt werden.
-Verteilung gemäß
(16.142) ermittelt werden.
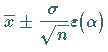 in
(16.139) heißen
Vertrauensgrenzen für den Mittelwert
in
(16.139) heißen
Vertrauensgrenzen für den Mittelwert ![]() ,
dann kann
in (16.139) an Stelle der in der Regel unbekannten Streuung
,
dann kann
in (16.139) an Stelle der in der Regel unbekannten Streuung ![]() der Grundgesamtheit die Stichprobenstreuung
der Grundgesamtheit die Stichprobenstreuung ![]() verwendet werden.
Anderenfalls müssen die Vertrauensgrenzen mit Hilfe der
verwendet werden.
Anderenfalls müssen die Vertrauensgrenzen mit Hilfe der ![]() -Verteilung gemäß
(16.142) ermittelt werden.
-Verteilung gemäß
(16.142) ermittelt werden.