Student-Verteilung
1. Dichte und Verteilungsfunktion:
Ist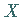 
eine (
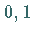)-normalverteilte Zufallsveränderliche und 
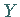eine von
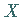unabhängige Zufallsveränderliche, die 
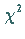-verteilt ist mit 
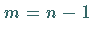Freiheitsgraden, so heißt die Verteilung der Zufallsgröße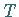 
 |
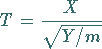(16.99) |
STUDENT-Verteilung oder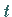 
-Verteilung mit 
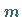Freiheitsgraden.
Die Verteilungsfunktion wird mit 
,
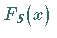die zugehörige Dichte mit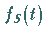 
bezeichnet.
Es gilt:
 |
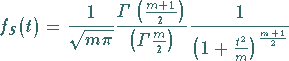(16.100a) |
 |
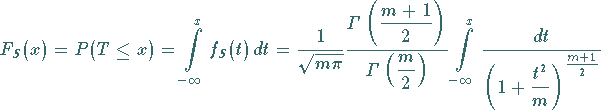(16.100b) |
2. Erwartungswert und Streuung:
 |
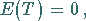(16.101a) |
 |
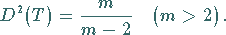(16.101b) |
3. Quantile:
Für die Quantile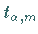 
bzw. 
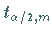der
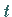-Verteilung (s. folgende zwei Abbildungen) gilt:
 |
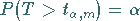(16.102a) |
oder
 |
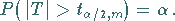(16.102b) |
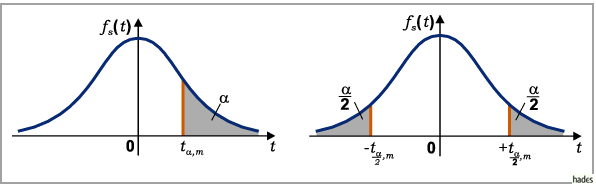
Die Quantile der STUDENT-Verteilung sind in der zugehörigen
Tabelle STUDENT-Verteilung zu finden.
Das Einsatzgebiet der STUDENT-Verteilung, die von GOSSET unter dem Pseudonym
STUDENT eingeführt wurde, sind Stichproben mit geringem Umfang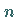 
,
für die
nur Schätzwerte des Erwartungswertes und der Standardabweichung angegeben werden
können.
Die Standardabweichung der Grundgesamtheit ist in (16.101b) nicht mehr enthalten.
