Mehrdimensionale Zufallsveränderliche
Ein Zufallsvektor 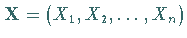 liegt vor, wenn jedes
Elementarereignis darin besteht, daß
liegt vor, wenn jedes
Elementarereignis darin besteht, daß 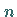 Zufallsveränderliche
Zufallsveränderliche
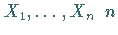 reelle Zahlenwerte
reelle Zahlenwerte 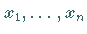 annehmen.
Die zugehörige Verteilungsfunktion wird durch
annehmen.
Die zugehörige Verteilungsfunktion wird durch
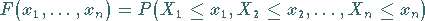 |
(16.58) |
beschrieben.
Sie heißt stetig, wenn eine Funktion 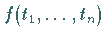 existiert, so daß
existiert, so daß
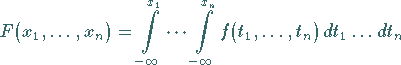 |
(16.59) |
gilt.
Die Funktion 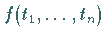 heißt die Dichte der Verteilung oder
Verteilungsdichte .
Läßt man einige der Variablen
heißt die Dichte der Verteilung oder
Verteilungsdichte .
Läßt man einige der Variablen 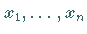 nach Unendlich streben, so
erhält man sogenannte Randverteilungen .
Genauere Untersuchungen und Beispiele findet man in Lit. 16.4 und
16.29.
nach Unendlich streben, so
erhält man sogenannte Randverteilungen .
Genauere Untersuchungen und Beispiele findet man in Lit. 16.4 und
16.29.
Von unabhängigen Zufallsveränderlichen 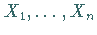 spricht man, wenn
gilt:
spricht man, wenn
gilt:
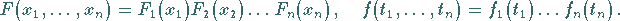 |
(16.60) |
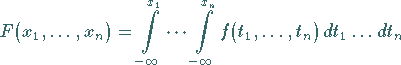
![]() spricht man, wenn
gilt:
spricht man, wenn
gilt: