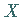|
|
|
|
wird durch ihre Verteilungsfunktion und deren Parameter
charakterisiert, wobei die Verteilungsfunktion ihrerseits durch die Eigenschaften der
Grundgesamtheit bestimmt ist.
Diese sind aber bei Beginn einer statistischen Untersuchung nicht bekannt, so daß man
möglichst viele Informationen mit Hilfe von Stichproben gewinnen muß.
In der Regel wird man sich nicht auf eine Stichprobe beschränken, sondern mehrere
Stichproben, praktischerweise vom gleichen Umfang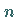 
,
untersuchen.
Dabei zeigt sich, daß die Realisierungen von Stichprobe zu Stichprobe unterschiedlich
ausfallen, d.h. der 1. Wert der 1. Stichprobe vom 1. Wert der 2. Stichprobe verschieden
sein wird usw.
Damit ist die Variable 1. Wert der Stichprobe ebenfalls eine Zufallsgröße, die mit
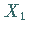bezeichnet wird.
Analog kann man für den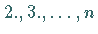 
-ten Stichprobenwert die Zufallsgröße
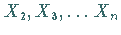einführen, die man auch Stichprobenvariable nennt.
Zusammengefaßt erhält man den Zufallsvektor
Jede konkrete Stichprobe vom Umfang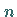 
mit den Elementen 
,
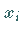die einer
Grundgesamtheit entnommen wurden, kann als Vektor
|
|