Vorgabe beliebiger Vertrauensgrenzen
Die Größe 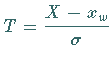 genügt im Falle einer
genügt im Falle einer 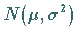 verteilten Grundgesamtheit der
verteilten Grundgesamtheit der 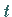 -Verteilung (16.100b) mit dem
Freiheitsgrad
-Verteilung (16.100b) mit dem
Freiheitsgrad 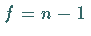 .
Für eine geforderte Irrtumswahrscheinlichkeit
.
Für eine geforderte Irrtumswahrscheinlichkeit 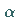 oder statistische Sicherheit
oder statistische Sicherheit
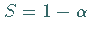 ergeben sich für den unbekannten wahren Wert
ergeben sich für den unbekannten wahren Wert  mit Hilfe
der
mit Hilfe
der 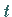 -Quantile
-Quantile 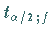 die Vertrauensgrenzen
die Vertrauensgrenzen
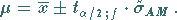 |
(16.217) |
Somit liegt der wahre Wert 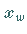 mit der statistischen Sicherheit
mit der statistischen Sicherheit 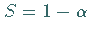 ,
d.h. mit der Wahrscheinlichkeit
,
d.h. mit der Wahrscheinlichkeit 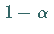 ,
innerhalb dieses Intervalls mit den
angegebenen Vertrauensgrenzen.
,
innerhalb dieses Intervalls mit den
angegebenen Vertrauensgrenzen.
Meist ist man daran interessiert, den Meßreihenumfang 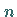 so gering wie möglich zu
halten.
Das Vertrauensintervall
so gering wie möglich zu
halten.
Das Vertrauensintervall 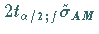 ist um so enger, je
kleiner
ist um so enger, je
kleiner 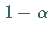 gewählt wird und je größer die Anzahl
gewählt wird und je größer die Anzahl 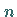 der Messungen ist.
Da
der Messungen ist.
Da 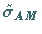 mit
mit 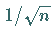 abnimmt und die Quantile
abnimmt und die Quantile
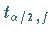 mit
mit 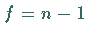 abnehmen (bei
abnehmen (bei 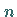 von 5 bis 10 ebenfalls mit
von 5 bis 10 ebenfalls mit
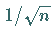 (s. Tabelle STUDENT-Verteilung)), verringert
sich die Breite des Vertrauensintervalls hier mit
(s. Tabelle STUDENT-Verteilung)), verringert
sich die Breite des Vertrauensintervalls hier mit 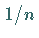 .
.
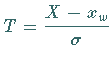 genügt im Falle einer
genügt im Falle einer