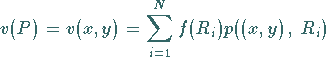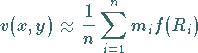Themen dieser Seite
Lösung partieller Differentialgleichungen durch Irrfahrtsprozesse
Mit Hilfe von Irrfahrtsprozessen wird die Monte-Carlo-Methode zur genäherten
Lösung von partiellen Differentialgleichungen realisiert.
Es wird die folgende Randwertaufgabe betrachtet:
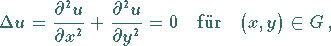 |
(16.182a) |
 |
(16.182b) |
Hierbei ist 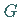 ein einfach zusammenhängendes Gebiet der
ein einfach zusammenhängendes Gebiet der 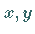 -Ebene; mit
-Ebene; mit
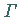 ist der Rand von
ist der Rand von 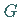 bezeichnet.
Wie bei den Differenzenmethoden im Abschnitt Differenzenverfahren
wird
bezeichnet.
Wie bei den Differenzenmethoden im Abschnitt Differenzenverfahren
wird 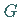 mit einem quadratischen Gitter überzogen, bei dem ohne Beschränkung der
Allgemeinheit die Schrittweite
mit einem quadratischen Gitter überzogen, bei dem ohne Beschränkung der
Allgemeinheit die Schrittweite  gewählt werden soll.
gewählt werden soll.
Auf diese Weise entstehen innere Gitterpunkte 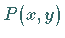 und Randpunkte
und Randpunkte 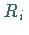 .
Von den Randpunkten
.
Von den Randpunkten 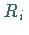 ,
die auch Gitterpunkte sind, wird zunächst zur Vereinfachung
angenommen, daß sie tatsächlich auf dem Rand
,
die auch Gitterpunkte sind, wird zunächst zur Vereinfachung
angenommen, daß sie tatsächlich auf dem Rand 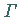 von
von 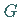 liegen, d.h., es soll
liegen, d.h., es soll
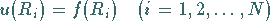 |
(16.183) |
gelten (s. Abbildung).
Lösungsprinzip
Man stellt sich vor, daß ein Teilchen von einem inneren Punkt 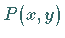 aus zu einer
Irrfahrt startet. Das bedeutet:
aus zu einer
Irrfahrt startet. Das bedeutet:
1. Das Teilchen bewegt sich von 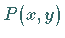 aus zufällig zu einem der 4
Nachbarpunkte des Gitters.
Jedem dieser 4 Gitterpunkte wird die Wahrscheinlichkeit
aus zufällig zu einem der 4
Nachbarpunkte des Gitters.
Jedem dieser 4 Gitterpunkte wird die Wahrscheinlichkeit 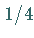 für eine Bewegung zu
diesem Punkt zugeordnet.
für eine Bewegung zu
diesem Punkt zugeordnet.
2. Erreicht das Teilchen einen Randpunkt 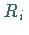 ,
dann endet dort die Irrfahrt mit
der Wahrscheinlichkeit 1.
,
dann endet dort die Irrfahrt mit
der Wahrscheinlichkeit 1.
Es läßt sich zeigen, daß ein Teilchen nach endlich vielen Schritten von einem
inneren Punkt 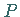 aus einen Randpunkt
aus einen Randpunkt 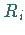 erreicht.
Mit
erreicht.
Mit
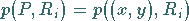 |
(16.184) |
wird die Wahrscheinlichkeit bezeichnet, daß eine Irrfahrt vom Punkt 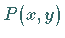 aus in
dem Randpunkt
aus in
dem Randpunkt 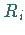 endet.
Dann gilt
endet.
Dann gilt
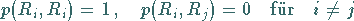 |
(16.185) |
und
Diese Gleichung (16.186) stellt eine Differenzengleichung für 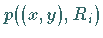 dar.
Werden
dar.
Werden 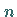 Irrfahrten vom Punkt
Irrfahrten vom Punkt 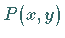 aus durchgeführt, von denen
aus durchgeführt, von denen 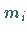 im Punkt
im Punkt
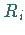 enden
enden 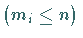 ,
dann gilt
,
dann gilt
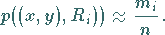 |
(16.187) |
Diese Gleichung (16.187) gibt eine Näherungslösung der Differentialgleichung
(16.182a) unter der Bedingung (16.183) an.
Die Randbedingung (16.182b) wird dagegen berücksichtigt, indem man
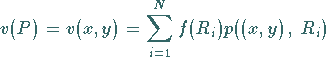 |
(16.188) |
setzt; denn wegen (16.186) gilt
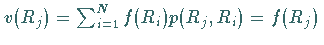 .
.
Zur Berechnung von 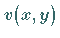 wird (16.186) mit
wird (16.186) mit 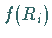 multipliziert.
Nach Summation erhält man die folgende Differenzengleichung für
multipliziert.
Nach Summation erhält man die folgende Differenzengleichung für 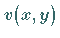 :
:
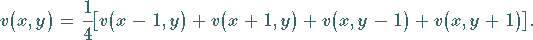 |
(16.189) |
Werden 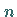 Irrfahrten vom inneren Punkt
Irrfahrten vom inneren Punkt 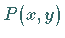 aus durchgeführt, von denen
aus durchgeführt, von denen 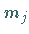 im
Randpunkt
im
Randpunkt 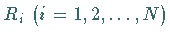 enden, dann erhält man durch
enden, dann erhält man durch
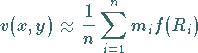 |
(16.190) |
einen Näherungswert im Punkt 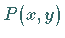 des Randwertproblems (16.182a,b).
des Randwertproblems (16.182a,b).