Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Benutzung der relativen Häufigkeit

Es soll angenommen werden, daß 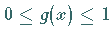gilt. Dies läßt sich durch die Transformation (16.177) stets erreichen. Dann gibt das Integral 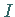den Inhalt einer Fläche an, die ganz im Einheitsquadrat 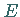liegt (s. Abbildung).



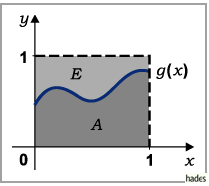
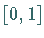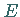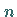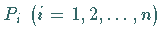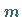Von einer Folge gleichverteilter Zufallszahlen aus dem Intervall faßt man je zwei zu den Koordinaten eines Punktes des Einheitsquadrates zusammen und erzeugt auf diese Weise Punkte . Bezeichnet man mit die Anzahl der Punkte, die innerhalb oder auf dem Rand der Fläche 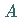liegen, dann gilt unter Beachtung des Begriffes der relativen Häufigkeit:
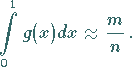(16.173)

Um mit Hilfe von (16.173) eine bestimmte Genauigkeit zu erreichen, ist eine sehr große Anzahl von Zufahlszahlen notwendig. Deshalb hat man nach Möglichkeiten zur Erhöhung der Effektivität gesucht. Eine davon stellt die folgende Monte-Carlo-Methode dar, weitere findet man in Lit. 16.22.