Da die Bildfunktion 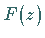 gemäß (15.109) eine Potenzreihe bezüglich der
komplexen Veränderlichen
gemäß (15.109) eine Potenzreihe bezüglich der
komplexen Veränderlichen 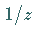 ist, folgt aus den Eigenschaften von
Potenzreihen im Komplexen:
ist, folgt aus den Eigenschaften von
Potenzreihen im Komplexen:
a) Für eine Z-transformierbare Folge 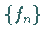 gibt es eine reelle Zahl
gibt es eine reelle Zahl 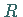 ,
so daß die Reihe (15.109) absolut konvergiert für
,
so daß die Reihe (15.109) absolut konvergiert für 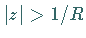 und
divergiert für
und
divergiert für 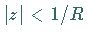 .
Für
.
Für 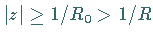 ist die Reihe sogar gleichmäßig konvergent.
Mit
ist die Reihe sogar gleichmäßig konvergent.
Mit 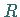 ist der Konvergenzradius der Potenzreihe (15.109) bezüglich
ist der Konvergenzradius der Potenzreihe (15.109) bezüglich 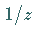 bezeichnet.
Konvergiert die Reihe für alle
bezeichnet.
Konvergiert die Reihe für alle 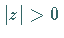 ,
so setzt man
,
so setzt man 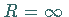 .
Für nicht Z-transformierbare Folgen setzt man
.
Für nicht Z-transformierbare Folgen setzt man 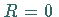 .
.
b) Ist 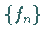 Z-transformierbar für
Z-transformierbar für 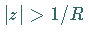 ,
dann ist die
zugehörige Bildfunktion
,
dann ist die
zugehörige Bildfunktion 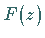 eine analytische Funktion für
eine analytische Funktion für 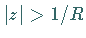 und
gleichzeitig die einzige Bildfunktion von
und
gleichzeitig die einzige Bildfunktion von 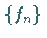 .
Für die Umkehrung gilt: Ist
.
Für die Umkehrung gilt: Ist 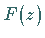 eine analytische Funktion für
eine analytische Funktion für 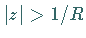 und
auch für
und
auch für 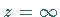 regulär, dann gibt es zu
regulär, dann gibt es zu 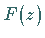 genau eine Originalfolge
genau eine Originalfolge
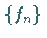 .
Dabei heißt
.
Dabei heißt 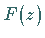 regulär für
regulär für 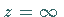 ,
wenn
,
wenn 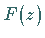 eine
Potenzreihenentwicklung der Form (15.109) besitzt und
eine
Potenzreihenentwicklung der Form (15.109) besitzt und 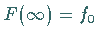 gilt.
gilt.