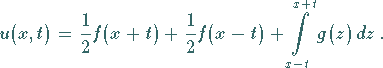1. Problemstellung
Die eindimensionale Wellengleichung mit verschwindendem Störglied und für ein
homogenes Medium lautet:
 |
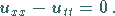(15.104a) |
Wie die dreidimensionale Wellengleichung (9.102a), so ist auch
15.104a eine partielle Differentialgleichung vom hyperbolischen Typ.
Das CAUCHYsche Problem sei durch die Anfangsbedingungen
 |
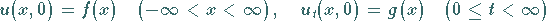(15.104b) |
korrekt gestellt.
2. Fourier-Transformation
Zur Lösung wird die FOURIER-Transformation bezüglich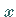 
durchgeführt, wobei
die Zeitkoordinate konstant gehalten wird:
 |
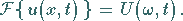(15.105a) |
Daraus ergibt sich:
 |
 |
 |
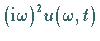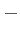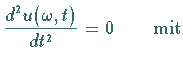(15.105b) |
 |
 |
 |
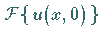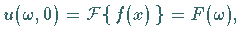(15.105c) |
 |
|
 |
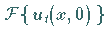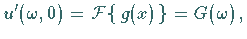(15.105d) |
 |
|
 |
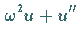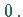(15.105e) |
Das Ergebnis ist eine gewöhnliche Differentialgleichung für die nun wieder als
Veränderliche zu betrachtende Zeitkoordinate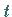 
mit dem Parameter 
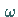der
Bildfunktion.
Die allgemeine Lösung dieser bekannten Differentialgleichung mit konstanten
Koeffizienten lautet
 |
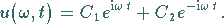(15.106a) |
Mit Hilfe der Anfangsbedingungen
 |
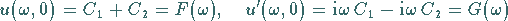(15.106b) |
lassen sich die Konstanten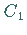 
und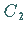 
bestimmen:
 |
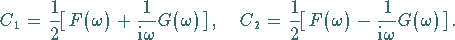(15.106c) |
Die Lösung ergibt sich zu
 |
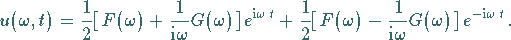(15.106d) |
3. Rücktransformation
Zur Rücktransformation der Funktion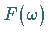 
kann der
Verschiebungssatz,
 |
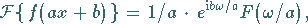(15.107a) |
mit Vorteil eingesetzt werden, woraus sich ergibt
 |
(15.107b) |
Die Anwendung der Integrationsregel
nach Substitution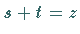 
und analog
 |
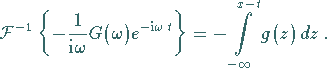(15.107e) |
Die endgültige Lösung im Originalbereich lautet somit
 |
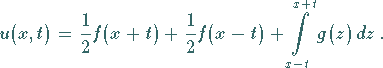(15.108) |
