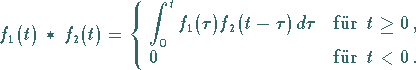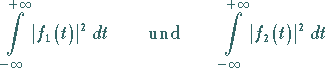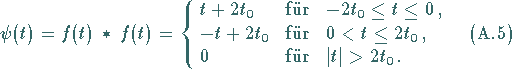|
Es ist die zweiseitige Faltung
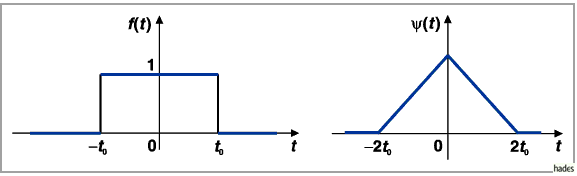
für die Funktion des unipolaren Rechteckimpulses (A.1) (linke
Abbildung) zu berechnen.
Da
gilt, ergibt sich
für 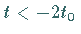 ,
für ,
für 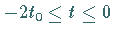 ,
für ,
für 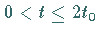 .
Zusammengefaßt erhält man für diese Faltung (rechte Abbildung)
Für die FOURIER-Transformierte erhält man mit (A.1)
vom Beisiel für den unipolaren Rechteckimpuls
und für das Amplitudenspektrum der Funktion .
Zusammengefaßt erhält man für diese Faltung (rechte Abbildung)
Für die FOURIER-Transformierte erhält man mit (A.1)
vom Beisiel für den unipolaren Rechteckimpuls
und für das Amplitudenspektrum der Funktion 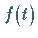
|