Die Lösung einer partiellen Differentialgleichung ist eine Funktion mindestens zweier
Variabler: 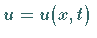 .
Da die LAPLACE-Transformation eine Integration bezüglich einer Variablen
darstellt, ist die andere Variable bei der Transformation als konstant zu betrachten:
.
Da die LAPLACE-Transformation eine Integration bezüglich einer Variablen
darstellt, ist die andere Variable bei der Transformation als konstant zu betrachten:
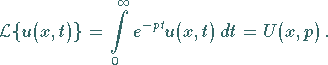 |
(15.56) |
Auch bei der Transformation von Ableitungen bleibt 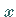 fest:
fest:
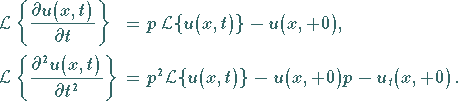 |
(15.57) |
Für die Ableitungen nach 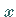 ist vorauszusetzen, daß sie mit dem
LAPLACE-Integral vertauschbar sind:
ist vorauszusetzen, daß sie mit dem
LAPLACE-Integral vertauschbar sind:
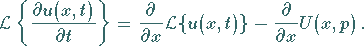 |
(15.58) |
Damit erhält man im Unterbereich eine gewöhnliche Differentialgleichung.
Außerdem sind die Rand- und Anfangsbedingungen in den Bildbereich zu transformieren.
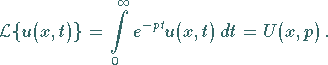
![]() fest:
fest:
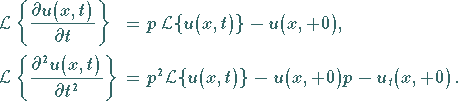
![]() ist vorauszusetzen, daß sie mit dem
LAPLACE-Integral vertauschbar sind:
ist vorauszusetzen, daß sie mit dem
LAPLACE-Integral vertauschbar sind: