Als Beispiel für eine diskrete Wavelet-Transformation wird die
HAAR-Wavelet-Transformation beschrieben:
Von einem Signal sind die Werte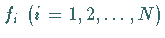 
gegeben.
Aus diesen werden die Detailwerte 
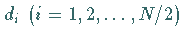wie folgt
berechnet:
 |
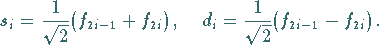(15.153) |
Die Werte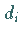 
werden abgespeichert, während auf die Werte 
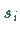die
Vorschrift (15.153) angewendet wird, d.h., in
(15.153) werden die Werte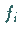 
durch die Werte
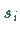ersetzt.
Diese Vorgehensweise wird fortgesetzt, so daß sich aus
 |
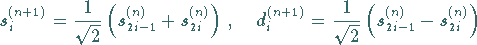(15.154) |
schließlich eine Folge von Detailvektoren mit den Komponenten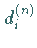 
ergibt.
Jeder Detailvektor enthält Informationen über Eigenschaften des Signals.
Hinweis: Für große Werte von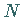 
konvergiert die diskrete
Wavelet-Transformation gegen die Integral-Wavelet-Transformation
(15.150a).
