Wavelets

Wavelets

Der FOURIER-Transformation fehlt eine Lokalisierungseigenschaft, d.h. ändert sich ein Signal an einer Stelle, dann ändert sich die Transformierte überall, ohne daß durch ,,einfaches Hinsehen`` die Stelle der Änderung gefunden werden kann. Der Grund liegt darin, daß die FOURIER-Transformation ein Signal in ebene Wellen zerlegt. Diese werden durch trigonometrische Funktionen beschrieben, die beliebig lange mit derselben Periode schwingen. Bei der Wavelet-Transformation dagegen wird eine fast beliebig wählbare Funktion

, das Wavelet (kleine lokalisierte Welle), zur Analyse eines Signals verschoben und gestaucht.

Beispiele für Wavelets sind:

Beispiel A

HAAR-Wavelet (s. die folgende Abbildung):

(15.143)

Beispiel B

Mexikanischer Hut (s. die folgende Abbildung).

(15.144)

Allgemein gilt: Als Wavelet kommen alle Funktionen in Frage, die quadratisch integrierbar sind und deren FOURIER-Transformierte gemäß (15.142a) zu einem positiven endlichen Integral

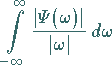(15.145)

führen. Im Zusammenhang mit Wavelets sind die folgenden Eigenschaften und Definitionen wichtig:

Mittelwert

1. Für den Mittelwert von Wavelets gilt:

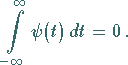(15.146)

2. Als

-tes Moment eines Wavelets

bezeichnet man das Integral

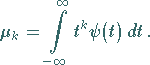(15.147)

Die kleinste positive natürliche Zahl

, für die

gilt, heißt Ordnung des Wavelets

Beispiel

Für das HAAR-Wavelet (15.143) gilt , für den mexikanischen Hut (15.144) .

3. Falls für alle gilt, ist von unendlicher Ordnung. Wavelets mit beschränktem Träger haben stets eine endliche Ordnung.
4. Ein Wavelet der Ordnung ist orthogonal zu allen Polynomen vom Grade .

Beispiel
	Für das HAAR-Wavelet (15.143) gilt , für den mexikanischen Hut (15.144) .