Analytische Funktion innerhalb eines Gebietes
Ist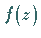 
auf einer geschlossenen Kurve 
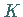und in dem von ihr umschlossenen einfach
zusammenhängenden Gebiet analytisch, dann gilt für jeden inneren Punkt 
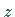dieses
Gebietes (s. Abbildung) die Darstellung
 |
(14.42) |
wenn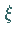 
die Kurve
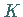im Gegenuhrzeigersinn durchläuft.
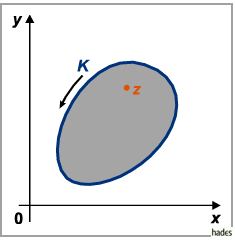
Somit lassen sich die Funktionswerte einer analytischen Funktion im Innern eines Gebietes
durch die Funktionswerte auf dem Rande des Gebietes ausdrücken.
Aus (14.42) ergeben sich Existenz und Integraldarstellung der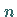 
-ten Ableitung
einer in einem Gebiet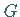 
analytischen Funktion:
 |
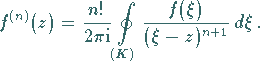(14.43) |
Eine analytische Funktion ist demnach beliebig oft differenzierbar.
Im Unterschied dazu folgt im Reellen aus der einmaligen Differenzierbarkeit nicht die
wiederholte Differenzierbarkeit.
Die Gleichungen (14.42) und (14.43) werden CAUCHYsche
Integralformeln genannt.
